le logo du site

4. Lois théoriques usuelles.

4.4.5. Lois de Student.

Le premier calcul de ce type de loi a été présenté par Helmert, ensuite Gosset a publié, en 1908, une forme générale sous le pseudonyme Student. Enfin Fisher les a utilisées dans des tests d’hypothèses sous le nom «lois de Student».

Définition 1. Soient \(Y, Z\) deux v.a. indépendantes, respectivement de loi Normale \({\cal L}(Y)={\cal N}(\delta\ ;\ 1)\) et de loi du Khi-deux \({\cal L}(Z)=\chi_n^2\). Nous posons :

\[ X=\frac{Y}{\sqrt{\displaystyle\frac{Z}{n}}}. \]

Si \(\delta=0\), alors la loi de \(X\) est une loi de Student à \(n\) degrés de liberté. Ceci est noté \({\cal L}(X)={\cal T}_n\). Si \(\delta\not=0\), alors la loi de \(X\) est une loi du Student non centrée à \(n\) degrés de liberté et avec un paramètre de non centralité \(\delta\). Ceci est noté \({\cal L}(X)={\cal T}_n(\delta)\).

Modélisation. Ces lois sont utilisées dans l’étude des moyennes observées. En particulier pour l’estimation de la moyenne théorique d’une loi Normale. Elles interviennent également dans les tests sur les moyennes de lois Normales, les lois de Student sous les hypothèses nulles et les lois de Student non centrées sous les contre-hypothèses (cf. la partie du site concernant ces tests).

Graphique 1. La Fig. 1 ci-dessous représente les courbes des densités de de la loi Normale Standard et de deux lois de Student, de paramètres différents.

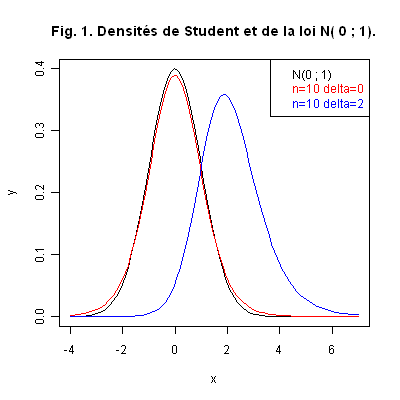
Densités de Student

Remarque 1. Nous constatons que la densité de la loi \({\cal T}_{10}\) (en rouge) est très proche de celle de la loi Normale Standard (en noir). En pratique dès que \(30\leq n\), nous pouvons confondre ces deux lois. À titre d’exemple, les commandes de R suivantes nous donnent la probabilité de ne pas dépasser 2 pour les deux lois.

pnorm(2, lower.tail=TRUE) ; réponse : 0.9772499.

pt(2, df=30, lower.tail=TRUE) ; réponse : 0.9726875.

Calculs avec R. Si \({\cal L}(X)={\cal T}_{10}\) et \({\cal L}(Y)={\cal T}_{10}(2)\), alors :

pt(2.5, df=10, ncp=0, lower.tail=TRUE)- pt(-2.5, df=10, ncp=0, lower.tail=TRUE)

donne \(P(-2,5<X\leq 2,5)=\)0.9685532.

pt(2.5, df=10, ncp=2, lower.tail=TRUE)- pt(-2.5, df=10, ncp=2, lower.tail=TRUE)

donne \(P(-2,5<Y\leq 2,5)=\)0.6479861.

qt(.75, df=10, lower.tail=TRUE) donne le troisième quartile \(Q_{0,75}\lbrack X\rbrack=\)0.699812.

qt(0.75, df=10, ncp=2, lower.tail=TRUE) donne le troisième quartile \(Q_{0,75}\lbrack Y\rbrack=\)2.873473.

Propriété 1. Si \({\cal L}(X)={\cal T}_n(\delta)\) alors :

\[ {\mathbb E}\lbrack X \rbrack =\delta\sqrt{\displaystyle\frac{n}{2}}\frac{\Gamma(\frac{n-1}{2})}{\Gamma(\frac{n}{2})}\quad \forall\ 1< n\quad {\it et}\quad \sigma^2\lbrack X\rbrack =(1+\delta^2)\frac{n}{n-2}\quad \forall\ 2< n. \]

Remarque 2. Lorsque \(\delta=0\), nous retrouvons le fait que la loi \({\cal T}_n\), pour \(1< n\), est centrée. De plus, toujours pour \({\cal T}_n\), avec cette fois-ci \(2< n\), nous retrouvons le fait que la variance est supérieure à 1 mais s’en rapproche lorsque \(n\rightarrow +\infty\).

Propriété 2. Lorsque \(n=1\), alors \({\cal T}_1(\delta)={\cal CA}(\delta\ ;\ 1)\), loi de Cauchy.

Remarque 3. C’est cette propriété qui explique la condition d’existence de la moyenne théorique d’une loi de Student.

Propriété 3. Si \({\cal L}(X)={\cal T}_n\) alors \(\gamma_1\lbrack X\rbrack =0\) pour \(3< n\) et \(\gamma_2\lbrack X\rbrack = \dfrac{6}{n-4}\) pour \(4< n\).

Remarque 4. Nous retrouvons ici, sous des conditions sur \(n\), le fait que les lois de Student sont symétriques par rapport à \(0\) et qu’elles sont leptokutiques, c’est-à-dire moins aplaties qu’une loi Normale.

Propriété 4. Si \({\cal L}(X)={\cal T}_n(\delta)\) alors \({\cal L}(X^2)={\cal F}_{1,n}(\delta)\), loi de Fisher.

Propriété 5. Si une v.a. \(X\) est de loi \({\cal L}(X)={\cal T}_n\), alors sa densité s’écrit :

\[ f_X(t)=\frac{\Gamma(\frac{n+1}{2})}{\sqrt{n\pi}\Gamma(\frac{n}{2})}(1+\frac{t^2}{n})^{-\frac{n+1}{2}}\quad \forall\ t\in {\mathbb R}. \] Haut de la page.