le logo du site

4. Lois théoriques usuelles.

4.4.6. Lois de Fisher - Snedecor.

Les premières lois dites de Fisher-Snedecor ont été proposées par Fisher. Leurs applications ont été développées par Snedecor.

Définition 1. Soit \(X_1, X_2\) deux v.a. indépendantes de loi \({\cal L}(X_1)=\chi_{n_1}^2(\delta)\) et \({\cal L}(X_2)=\chi_{n_2}^2\) respectivement. Nous posons :

\[ X=\frac{\displaystyle\frac{X_1}{n_1}}{\displaystyle\frac{X_2}{n_2}}. \]

Si \(\delta=0\), alors la loi de \(X\) est une loi de Fisher - Snedecor à \(n_1, n_2\) degrés de liberté. Nous pouvons également dire plus simplement loi de Fisher ou encore loi F de Fisher et éventuellement préciser \(n_1\) degrés de liberté au numérateur et \(\ n_2\) degrés de liberté au dénominateur. Ceci est noté \({\cal L}(X)={\cal F}_{n_1,\ n_2}\). Si \(\delta\not=0\), alors la loi de \(X\) est une loi de Fisher - Snedecor excentrée à \(n_1, n_2\) degrés de liberté et avec un paramètre d’excentricité \(\delta\). Ceci est noté \({\cal L}(X)={\cal F}_{n_1,\ n_2}(\delta)\).

Modélisation. Ces lois sont utilisées dans la comparaison de variances. En particulier pour l’estimation du rapport de deux variances théoriques de deux lois Normales. Elles interviennent également dans les tests sur les variances de lois Normales : les lois de Fisher - Snedecor sous les hypothèses nulles et les lois de Fisher - Snedecor excentrées sous les contre-hypothèses (cf. la partie du site concernant ces tests). Mais la plus importante utilisation des ces lois concerne les modèles linéaires normaux et les analyses de variance en particulier.

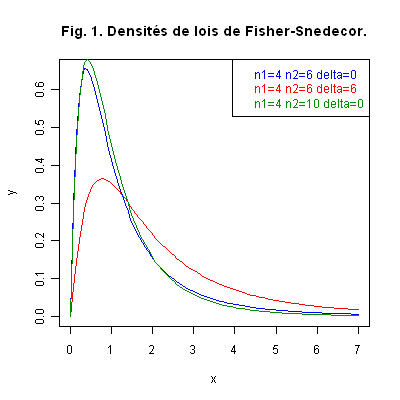
Graphique 1. La Fig. 1 ci-dessous représente les courbes des densités de lois du F de Fisher : \({\cal L}(X)={\cal F}_{4, 6}\), \({\cal L}(X)={\cal F}_{4, 6}(6)\) et \({\cal L}(X)={\cal F}_{4, 10}\).

Densité de Fisher-Snedecor

Calculs avec R. À la base, les commandes comprennent l’expression «f» précédée de la lettre spécifiant le calcul à réaliser : «d» pour le calcul de la densité, «p» pour le calcul d’une probabilité, «q» pour le calcul d’un quantile et «r» pour une simulation. Les options «df1», «df2» et «ncp» de la commande contiennent respectivement \(n_1\), \(n_2\) et \(\delta\) (par défaut «ncp=0»). Par exemple, si \({\cal L}(X)={\cal F}_{4,\ 6}\) alors, les quantiles les plus utilisés sont :

qf(0.025, df1=4, df2=6, lower.tail=TRUE) donne le quantile d’ordre 2,5 % : \(Q_X(0,025)=\)0.1087274.

qf(0.05, df1=4, df2=6, lower.tail=TRUE) donne le quantile d’ordre 5 % : \(\ Q_X(0,05)=\)0.1622552.

qf(0.95, df1=4, df2=6, lower.tail=TRUE) donne le quantile d’ordre 95 % : \(\ Q_X(0,95)=\)4.533677.

qf(0.9755, df1=4, df2=6, lower.tail=TRUE) donne le quantile d’ordre 97,5 % : \(Q_X(0,975)=\)6.227161.

Propriété 1. Si \({\cal L}(X)={\cal F}_{n_1,\ n_2}(\delta)\) alors :

\[ {\mathbb E}\lbrack X \rbrack =\frac{n_2(n_1+\delta)}{n_1(n_2-2)}\quad \forall\ 2< n_2,\quad \sigma^2\lbrack X\rbrack =2(\frac{n_2}{n_1})^2\frac{(n_1+\delta)^2+(n_1+2\delta)(n_2-2)}{(n_2-2)^2(n_2-4)}\quad \forall\ 4< n_2. \]

Remarque 1. Lorsque \(\delta=0\), nous avons une moyenne théorique qui ne dépend pas du degré de liberté du numérateur.

Propriété 2. Si \({\cal L}(X)={\cal F}_{n_1,\ n_2}\) alors \({\cal L}(\dfrac{1}{X})={\cal F}_{n_2,\ n_1}\).

Nous en déduisons la propriété suivantes :

Propriété 3. Si \({\cal L}(X)={\cal F}_{n_1,\ n_2}\) et \(Q_X(p)\) est le quantile d’ordre \(p\), c’est-à-dire \(P(X\leq Q_X(p))=p\), alors :

\[ Q_{\frac{1}{X}}(1-p)=\frac{1}{Q_X(p)}\quad {\it i.e.}\quad P(\frac{1}{X}\leq Q_{\frac{1}{X}}(1-p))=1-p. \]

Propriété 4. Si une v.a. \(X\) est de loi \({\cal L}(X)={\cal F}_{n_1,\ n_2}(\delta)\), alors sa densité s’écrit :

\[ f_X(t)=e^{-\frac{\delta}{2}}\sum_{j=0}^{+\infty}\frac{\delta^j}{j!2^j}\frac{n_1^{j+\frac{n_1}{2}} n_2^{\frac{n_1}{2}} t^{j-1-\frac{n_1}{2}}}{B(j+\frac{n_1}{2}\ ;\ \frac{n_2}{2}) (n_1+tn_2)^{j+\frac{n_1+n_2}{2}}} I_{\rbrack 0\ ;\ +\infty\lbrack}(t), \]

où \(B(n_1\ ;\ n_2)\) est la fonction bêta.

Remarque 2. Lorsque \(\delta=0\), il n’y a plus que le premier terme dans la somme et nous avons la densité de la loi \({\cal F}_{n_1,\ n_2}\). Les lois de Fisher - Snedecor excentrées sont liées aux lois Bêta excentrées, qui ne sont pas étudiées dans notre site.

Haut de la page.