Lois Normales à une dimension.

4.4.1. Lois Normales à une dimension.

Ces lois introduites indépendamment par Gauss et par Laplace sont les plus fréquemment rencontrées dans la nature. De ce fait leur importance en Statistique est primordiale. Nous pouvons affirmer que sans elles la Statistique n’existerait pas.

Définition 1. Une v.a. continue \(X\) suit une loi de Gauss, ou de Laplace - Gauss ou encore une loi Normale, de paramètres \(\mu\in {\mathbb R}\) et \(\sigma \in {\mathbb R}_+^{\star}\) si elle admet pour densité de probabilité la fonction :

\[ f_X(t) =\frac{1}{\sigma \sqrt{2\pi}}\exp\left(\displaystyle - \frac{1}{2\sigma^2} (t-\mu)^2\right),\quad t\in {\mathbb R}. \]

Ceci est noté \({\cal L}(X)={\cal N}(\mu\ ;\ \sigma^2)\). Si \(\mu=0\) et \(\sigma=1\), nous dirons que \(X\) suit la loi Normale centrée et réduite, ou encore la loi Normale standard, \({\cal N}(0\ ;\ 1)\).

Modélisation. Lorsqu’une mesure ou observation est le cumul d’un très grand nombre d’autres variables, indépendantes entres elles et individuellement négligeables, alors cette mesure peut être la réalisation d’une v.a. \(X\) qui suit une loi \({\cal N}\). Cette propriété, connue sous le nom de Théorème de la Limite Centrale, est celle qui donne toute son importance à la loi Normale.

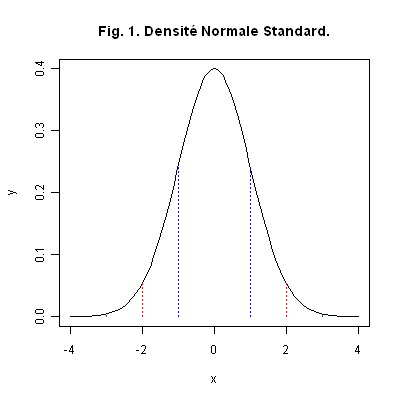
Graphique 1. La Fig. 1 ci-dessous représente la courbe d’une densité de loi Normale gaussienne \({\cal L}(X)={\cal N}(\mu\ ;\ \sigma^2)\), avec \(\mu=0\) et \(\sigma=1\). Elle est en forme de cloche, symétrique par rapport à la droite verticale d’abscisse \(t=0\), point où elle atteint son maximum qui vaut \(\displaystyle \frac{1}{\sigma \sqrt{2\pi}}\) avec, dans notre exemple \(\sigma=1\). Elle admet des points d’inflexion aux abscisses \(\mu \pm \sigma\), qui valent dans notre exemple \(\pm 1\) respectivement ; nous avons tracé des droites verticales bleues pour matérialiser ces points d’inflexion de la courbe. Cette dernière s’écrase très rapidement sur l’axe des abscisses, à partir de \(\mu \pm 4\sigma = \pm 4\) ici. Nous avons tracé des droites verticales rouges, respectivement vertes, à la verticale des points d’abscisse \(\mu\pm 2\sigma=\pm 2\), respectivement \(\mu\pm 3\sigma=\pm 3\). Nous reviendrons sur ces points remarquables.

Propriété 1. Si \({\cal L}(X)={\cal N}(\mu\ ;\sigma^2)\) alors :

\[ {\mathbb E}\lbrack X \rbrack = \mu =Me\lbrack X\rbrack = Mo\lbrack X\rbrack ,\quad \sigma^2\lbrack X\rbrack =\sigma^2, \] \[ Q_{0,25}\lbrack X\rbrack=\mu-0,6745\sigma,\quad Q_{0,75}\lbrack X\rbrack=\mu+0,6745\sigma,\quad \gamma_1\lbrack X\rbrack = 0,\quad \gamma_2\lbrack X\rbrack = 0, \]

\[ \mu_m={\mathbb E}\lbrack (X-\mu)^m \rbrack = \cases{ 0 &\({\it si}\quad m=2k+1\quad {\it est\ impair}\),\cr \displaystyle\frac{(2k)!\sigma^{2k}}{2^k k!} & \({\it si}\quad m=2k\quad {\it est\ pair}\). } \]

De plus la variable \( Z=\displaystyle \frac{X-\mu}{\sigma}\) est dite variable standardisée ; nous avons alors \({\cal L}(Z)={\cal N}(0\ ;\ 1)\). La fonction génératrice des moments est \( g_X(t)= \exp{(\mu t+\displaystyle\frac{\sigma^2t^2}{2})}\). La fonction caractéristique est \( \phi_X(t)= \exp{(i\mu t-\displaystyle\frac{\sigma^2t^2}{2})}\)

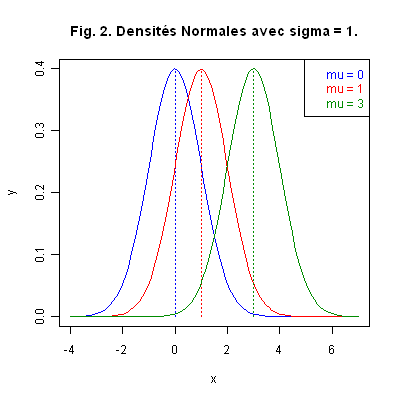
Graphique 2. Le paramètre \(\mu\), premier paramètre défini précédemment, correspond à l’espérance de la loi. À titre d’exemple, la Fig. 2 ci-dessous donne les courbes des densités de trois lois Normales de moyennes théoriques différentes mais de même écart type. Nous avons matérialisé les différentes espérances par des droites verticales, aux couleurs des densités, pour montrer les décalages.

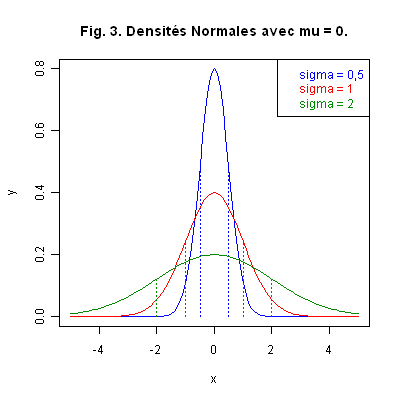
Graphique 3. Le paramètre \(\sigma\), deuxième paramètre défini précédemment, correspond à l’écart type de la loi. À titre d’exemple, la Fig. 3 ci-dessous donne les courbes des densités de trois lois Normales de même moyenne théorique mais d’écart type différent. Nous avons matérialisé les différents écarts types par des droites verticales, aux couleurs des densités, correspondant chaque fois aux abscisses \(\mu \pm \sigma\), pour montrer les différences d’étalement.

Calculs avec R. A la base, les commandes comprennent l’expression «norm» précédée d’une lettre spécifiant le calcul à réaliser. Les options «mean» et «sd» de la commande donnent respectivement \(\mu\) et \(\sigma\). Par exemple, si \({\cal L}(X)={\cal N}(10\ ;\ 2^2)\), alors \(f_X(11,6)\) se détermine avec la commande :

dnorm(11.6,mean=10,sd=2) ; réponse : 0.1448458.

Si \({\cal L}(X)={\cal N}(\mu\ ;\ \sigma^2)\) et \( Z=\displaystyle \frac{X-\mu}{\sigma}\), nous savons que \({\cal L}(Z)={\cal N}(0\ ;\ 1)\). Alors \(P(X\le \mu +1,28\sigma )= P(Z\le 1,28)\) se détermine avec la commande :

pnorm(1.28,lower.tail=TRUE) ; réponse : 0.8997274.

De même \(P(X\le \mu +1,64\sigma )= P(Z\le 1,64)\) se détermine avec la commande :

pnorm(1.64,lower.tail=TRUE) ; réponse : 0.9494974.

De même \(P(X\le \mu +1,96\sigma )= P(Z\le 1,96)\) se détermine avec la commande :

pnorm(1.96,lower.tail=TRUE) ; réponse : 0.9750021.

Remarque 1. Ces trois nombres \(1,28\), \(1,64\) et \(1,96\) interviendront dans les valeurs critiques de certains tests d’hypothèses.

De même \(P(\mu - \sigma\le X\le \mu + \sigma )= P(-1\le Z\le 1)\) se détermine avec la commande :

pnorm(1,lower.tail=TRUE)-pnorm(-1,lower.tail=TRUE) ; réponse : 0.6826895.

Remarque 2. Ainsi dans le graphique Fig. 3 ci-dessus, les aires comprises entre l’axe des abscisses, la densité et les droites verticales de même couleur, correspondant chaque fois aux abscisses \(\mu \pm \sigma\), sont toutes égales à 0,6826895.

De plus \(P(\mu - 2\sigma\le X\le \mu + 2\sigma )= P(-2\le Z\le 2)\) se détermine avec la commande :

pnorm(2,lower.tail=TRUE)-pnorm(-2,lower.tail=TRUE) ; réponse : 0.9544997.

De même \(P(\mu - 3\sigma\le X\le \mu + 3\sigma )= P(-3\le Z\le 3)\) se détermine avec la commande :

pnorm(3,lower.tail=TRUE)-pnorm(-3,lower.tail=TRUE) ; réponse : 0.9973002.

De même \(P(\mu - 4\sigma\le X\le \mu + 4\sigma )= P(-4\le Z\le 4)\) se détermine avec la commande :

pnorm(4,lower.tail=TRUE)-pnorm(-4,lower.tail=TRUE) ; réponse : 0.9999367.

Remarque 3. La commande «pnorm» avec l’option «lower.tail=TRUE», donne la probabilité d’observer une valeur inférieure à celle indiquée dans la commande ; elle est égale à l’aire comprise entre la densité et l’axe des abscisses et à gauche de la droite verticale d'abscisse la valeur donnée. C’est pourquoi, pour calculer la probabilité d’observer une valeur comprise dans un intervalle, nous faisons la différence des aires se trouvant à gauche des extrémités de l’intervalle.

Inteprétation. De ces résultats numériques nous déduisons que, «théoriquement», pour une variable de loi Normale,
- 68,3 % des observations sont dans l’intervale \(\lbrack \mu - \sigma\ ;\ \mu + \sigma \rbrack\) ;
- 95,5 % des observations sont dans l’intervale \(\lbrack \mu - 2\sigma\ ;\ \mu + 2\sigma \rbrack\) ;
- 99,7 % des observations sont dans l’intervale \(\lbrack \mu - 3\sigma\ ;\ \mu + 3\sigma \rbrack\) ;
Au-delà de \(\mu\pm 3\sigma\), il ne devrait plus y avoir d’observations. Si c’est le cas, cela veut dire que la loi Normale considérée n’est pas adéquate ou qu’elle n’a pas le bon écart type ou encore que l’observation qui se trouve au-delà est suspecte. Ces propriétés sont utilisées en contrôle de la qualité.

Les quantiles peuvent se calculer avec la commande suivante. Par exemple le troisième quartile de la loi Normale Standard est :

qnorm(.75,lower.tail=TRUE) ; réponse : 0.6744898.

Il est possible de réaliser des simulations d’observations d’une loi Normale avec la commande rnorm et les paramètres souhaités.

Propriété 2. Soit deux v.a. \(X_1\) et \(X_2\) telles que loi du couple \(\ ^t(X_1\ ;\ X_2)\) soit Normale régulière, c’est-à-dire que leur coefficient de corrélation n’est pas égal à \(\pm 1\) (cf. la page sur les Lois Normales multivariées). Nous notons leur loi, respectivement, \({\cal N}(\mu_1\ ;\sigma_1)\) et \({\cal N}(\mu_2\ ;\sigma_2)\). Pour tous nombres réels \(a, b\) nous avons alors :

\[ {\cal L}(aX_1+bX_2)={\cal N}\left(a\mu_1+b\mu_2\ ;\ a^2\sigma^2_1+b^2\sigma^2_2+a b {\mathbb C}ov\lbrack X_1\ ;\ X_2\rbrack\right). \]

En particulier, si \(X_1, \cdots, X_n\) sont des v.a. de même loi \({\cal L}(X)={\cal N}(\mu\ ;\sigma^2)\) et indépendantes, alors

\[ {\cal L}\left(\frac{1}{n} (X_1+\cdots+X_n)\right)={\cal N}\left(\mu\ ;\ \frac{\sigma^2}{n}\right). \] Haut de la page.

4. Lois théoriques usuelles.

4. Lois théoriques usuelles.

4.4.1. Lois Normales à une dimension.