

Les premières lois du Khi-deux ont été mentionnées par Helmert puis développées par Pearson.
Définition 1. Soit \(X_1, \cdots, X_n\) des v.a. indépendantes de loi Normale \({\cal N}(\mu_i\ ;\ 1), i=1, \cdots, n,\) respectivement. Nous posons :
\[ X=\sum_{i=1}^n X_i^2. \]Si \(\mu_1=\cdots=\mu_n=0\), alors la loi de \(X\) est une loi du Khi-deux à \(n\) degrés de liberté. Ceci est noté \({\cal L}(X)=\chi_n^2\).
Si au moins un des \(\mu_i, i=1, \cdots, n\), n’est pas nul, alors la loi de \(X\) est une loi du Khi-deux excentrée à \(n\) degrés de liberté et avec un paramètre d’excentricité \(\delta\)\(=\displaystyle\sum_{i=1}^n \mu_i^2\). Ceci est noté \({\cal L}(X)=\chi_n^2(\delta)\).
Modélisation. Ces lois sont utilisées dans l’étude des écarts quadratiques, en particulier pour l’estimation de variances. Elles interviennent également dans les tests sur les variances, les lois du Khi-deux sous les hypothèses nulles et les lois du Khi-deux excentrées sous les contre-hypothèses (cf. la partie du site concernant ces tests).
Graphique 1. La Fig. 1 ci-dessous représente les courbes de plusieurs densités de lois du Khi-deux de paramètres différents.
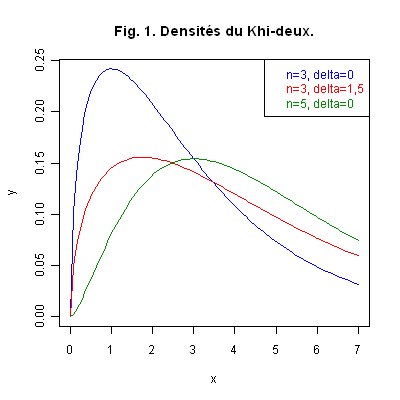
Calculs avec R. A la base, les commandes comprennent l’expression «chisq» précédée de la lettre spécifiant le calcul à réaliser : «d» pour le calcul de la densité, «p» pour le calcul d’une probabilité, «q» pour le calcul d’un quantile et «r» pour une simulation. Les options «df» et «ncp» de la commande donnent respectivement \(n\) et \(\delta\) (par défaut «ncp=0»). Par exemple, si \({\cal L}(X)=\chi_3^2\) et \({\cal L}(Y)=\chi_3^2(1,5)\), alors :
pchisq(3.5, df=3, ncp=0, lower.tail=TRUE) donne \(P(X\leq 3,5)=\)0.6792379.
pchisq(3.5, df=3, ncp=1.5, lower.tail=TRUE) donne \(P(Y\leq 3,5)=\)0.4782336.
qchisq(0.5, df=3, ncp=0, lower.tail=TRUE) donne la médiane \(Me\lbrack X\rbrack=\)2.365974.
qchisq(0.5, df=3, ncp=1.5, lower.tail=TRUE) donne la médiane \(Me\lbrack Y\rbrack=\)3.668745.
Propriété 1. Si \({\cal L}(X)=\chi_n^2(\delta)\) alors \({\mathbb E}\lbrack X \rbrack = n+\delta\) et \(\sigma^2\lbrack X\rbrack =2n+4\delta\). De plus la fonction génératrice des moments est
\[ g_X(t)= \frac{1}{(1-2t)^\frac{n}{2}}\exp(\frac{t\delta}{1-2t}),\quad \forall t < \frac{1}{2}. \]Remarque 1. Une loi du Khi-deux est une loi Gamma. De même, une loi du Khi-deux excentrée est une loi Gamma excentrée, loi que nous n’abordons pas dans ce site.
Propriété 2. Si deux v.a. \(X,\ Y\) sont indépendantes et de loi \({\cal L}(X)={\cal N}(\mu\ ;\ 1)\) et \({\cal L}(Y)=\chi_n^2\) alors :
\[ {\cal L}(X^2+Y)=\chi_{n+1}^2(\mu^2). \]Propriété 3. Si deux v.a. \(X_1,\ X_2\) sont indépendantes et de loi \({\cal L}(X_1)=\chi_{n_1}^2(\delta_1)\) et \({\cal L}(X_2)=\chi_{n_2}^2(\delta_2)\) alors :
\[ {\cal L}(X_1+X_2)=\chi_{n_1+n_2}^2(\delta_1+\delta_2). \]Propriété 4. Si un v.a. \(X\) est de loi \({\cal L}(X)={\cal N}_p(\mu\ ;\ \Sigma)\) régulière et \(\mu_1\in {\mathbb R}^p\) quelconque, alors :
\[ {\cal L}\left(\sideset{^t}{}(X-\mu_1)\Sigma^{-1}(X-\mu_1)\right)=\chi_{p}^2\left(\sideset{^t}{}(\mu-\mu_1)\Sigma^{-1}(\mu-\mu_1)\right), \]où \(d_M^2(\mu, \mu_1)=\sideset{^t}{}(\mu-\mu_1)\Sigma^{-1}(\mu-\mu_1)\) est appelée \(\Sigma-\)distance de Mahalanobis entre \(\mu\) et \(\mu_1\).
Cette distance due à Mahalanobis est très utilisée dans l’étude statistique des lois normales multivariées et en Analyse Discriminante.
Propriété 5. Si une v.a. \(X\) est de loi \({\cal L}(X)=\chi_{n}^2(\delta)\), alors sa densité s’écrit :
\[ f_X(t)=e^{-\frac{t+\delta}{2}}\sum_{j=0}^{+\infty} (\frac{\delta}{2})^j\frac{t^{\frac{n}{2}+j-1}}{j!\ 2^{\frac{n}{2}+j}\ \Gamma(\frac{n}{2}+j)} I_{\rbrack 0\ ;\ +\infty\lbrack}(t). \]Remarque 2. Lorsque \(\delta=0\), il n’y a plus que le premier terme dans la somme et nous reconnaissons la densité de la loi Gamma \({\cal GA}(\displaystyle\frac{n}{2}\ ;\ \frac{1}{2})\).
Intervalle de prédiction. Nous avons créé une procédure dans R qui permet de déterminer un intervalle de prédiction pour les lois du Khi-deux. Considérons la loi \(\chi_2^2\) à \(2\) degrés de liberté. Nous utilisons la procédure en indiquant le degré de liberté de la loi et le seuil de signification de l’intervalle ; voici le résultat :
KhideuxInterPred(2, 0.05) ; réponse :
Intervalle de prédiction de la loi Khi-deux( 2 ),
Seuil de l'intervalle : 5 %,
Intervalle : [ 0 ; 5.991465 ].
Nous en déduisons que \(I_{pred}(\chi_2^2\ ;\ 0,05)=\lbrack 0,000000\ ;\ 5,991465\rbrack\). Considérons la loi du Khi-deux \(\chi_9^2\). Nous avons :
KhideuxInterPred(9, 0.05) ; réponse :
Intervalle de prédiction de la loi Khi-deux( 9 ),
Seuil de l'intervalle : 5 %,
Intervalle : [ 1.902587 ; 17.39227 ].
Ainsi nous en déduisons que \(I_{pred}(\chi_9^2\ ;\ 0,05)=\lbrack 1,902587\ ;\ 17,392266\rbrack\). Considérons la loi du Khi-deux \(\chi_{20}^2\). Nous avons :
KhideuxInterPred(20, 0.05) ; réponse :
Intervalle de prédiction de la loi Khi-deux( 20 ),
Seuil de l'intervalle : 5 %,
Intervalle : [ 8.584137 ; 32.60721 ].
Nous en déduisons donc que l’intervalle de prédiction est : \(I_{pred}(\chi_{20}^2\ ;\ 0,05)=\lbrack 8,584137\ ;\ 32,607205\rbrack\). Ainsi nous constatons que l’intervalle est d’autant plus réduit que le degré de liberté est faible. Ceci est tout à fait naturel, rappelons en effet que pour une v.a. \(X\) qui suit une loi \(\chi_n^2\) l’espérance est \({\mathbb E}\lbrack X\rbrack=n\) et la variance \({\mathbb V}ar\lbrack X\rbrack=2n\). Remarquons également que lorsque le degré de liberté est \(n\leq 2\), le mode est \(0\) et la densité est toujours décroissante, ce qui nous donne des intervalles de prédiction du type \(I_{pred}(\chi_n^2\ ;\ \alpha)=\lbrack 0\ ;\ \overline{c}\rbrack. \quad\square\)
Haut de la page.