Lois de Gumbel.

4.9. Lois de Gumbel.

Les lois introduites par Gumbel sont très utiles pour l’étude des valeurs extrêmes.

Définition 1. Une v.a. continue \(X\) suit une loi de Gumbel de paramètres \(\lambda \in {\mathbb R},\ \delta\in {\mathbb R}_+^{\star}\) si elle admet pour densité de probabilité la fonction :

\[ \forall t\in {\mathbb R},\quad f_X(t) =\frac{1}{\delta} \exp(-\frac{t-\lambda}{\delta})\exp(-\exp(-\frac{t-\lambda}{\delta})). \]

Ceci est noté \({\cal L}(X)={\cal GU}(\lambda\ ;\ \delta)\). Lorsque \(\lambda=0\) et \(\delta=1\), nous disons que \({\cal GU}(0\ ;\ 1)\) est une loi de Gumbel standard.

Modélisation. Les loi de Gumbel peuvent décrire des phénomènes extrêmes de durée de vie, de coûts de sinistres en assurance, de crues de rivières, etc.

Calculs. Nous créons dans R une procédure que nous nommons GumbelDensite et qui permet de calculer la densité d’une loi \({\cal GU}(\lambda\ ;\ \delta)\). Après avoir «sourcée» cette procédure dans R, nous calculons, à titre d’exemple, pour \({\cal GU}(2\ ;\ 1)\), les valeurs de \(f(0), f(1)\) et \(f(3)\) :

GumbelDenisite(0, 2, 1) ; réponse : 0.004566281
GumbelDenisite(1, 2, 1) ; réponse : 0.1793741
GumbelDensite(3, 2, 1) ; réponse : 0.2546464

Graphique 1. La Fig. 1 ci-dessous représente les courbes des densités des lois de Gumbel \({\cal GU}(1\ ;\ 1)\), \({\cal GU}(2\ ;\ 1)\) et \({\cal GU}(1,5\ ;\ 2)\). Nous voyons évoluer l’allure de la densité en fonction des paramètres.

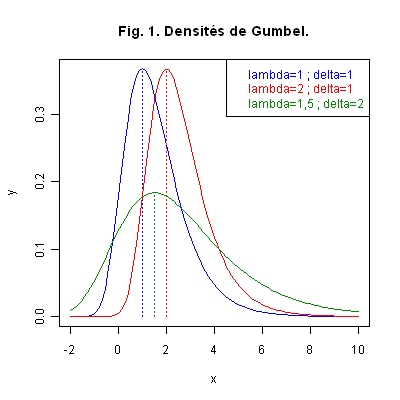
Remarque 1. La densité n’est pas symétrique ; elle admet un maximum égal à \(\displaystyle\frac{1}{e\delta}\) pour \(t=\lambda\) ; elle admet également deux points d’inflexion pour :

\[ \lambda-\delta\ln(\frac{3\pm \sqrt{5}}{2})\approx\lambda\pm 0,962424\ \delta. \]

Propriété 1. Si \({\cal L}(X)={\cal GU}(\lambda\ ;\ \delta)\) alors sa f.r. est :

\[ \forall t\in {\mathbb R},\quad F_X(t) = \exp(-\exp(-\frac{t-\lambda}{\delta})), \]

sa fonction génératrice des moments est :

\[ \forall t\in\rbrack -\infty\ ;\ \frac{1}{\delta}\lbrack,\quad M_X\lbrack X\rbrack = {\mathbb E}\lbrack \exp(tX)\rbrack=\Gamma(1-t\delta)\exp(\lambda t), \]

où \(\Gamma(u)\) est la fonction Gamma. Si nous posons \(Z=\displaystyle\frac{X-\lambda}{\delta}\) alors la loi de \(Z\) est une loi de Gumbel standard.

Propriété 2. Soit \({\cal L}(X)={\cal GU}(\lambda\ ;\ \delta)\). Nous posons \(Y=\dfrac{1}{\beta}\ \exp(-\dfrac{X-\lambda}{\delta})\) ou, ce qui est équivalent, \(X=\lambda -\delta\ \ln(\beta\ Y)\). Alors la loi de \(Y\) est une loi Exponentielle \({\cal L}(Y)={\cal GA}(1\ ;\ \beta)\).

Propriété 3. Si \({\cal L}(X)={\cal GU}(\lambda\ ;\ \delta)\) alors nous avons :

\[ {\mathbb E}\lbrack X\rbrack= \lambda-\Gamma^{\prime}(1)\delta=\lambda-\gamma\ \delta\approx\lambda - 0,577212\ \delta,\quad {\mathbb V}ar\lbrack X\rbrack= \frac{\delta^2\pi^2}{6}\approx1,644934\ \delta^2, \] \[ Mo\lbrack X\rbrack = \lambda \quad {\it et}\quad Me\lbrack X\rbrack=\lambda-\delta\ln(\ln(2))\approx\lambda-0,366513\ \delta, \]

où \(\gamma\approx 0,577212\) est la constante d’Euler.

Propriété 4. Si \(X_{\bullet}\) est un \(n-\)échantillon d’une v.a. \(X\) de loi \({\cal GU}(\lambda\ ;\ \delta)\), alors nous avons :

\[ {\cal L}(X_{(n)})= {\cal L}(\max_{i=1}^n X_i)={\cal GU}(\lambda+\delta\ln(n)\ ;\ \delta). \]

Pour le voir il suffit de calculer la f.r. du maximum.\(\quad \square\)

Propriété 5. Soit \(X_{\bullet}\) est un \(n-\)échantillon d’une v.a. \(X\) de f.r. \(F\), telle qu’il exite deux suites de nombres réels \((\alpha_n\ ;\ n\in{\mathbb N})\) et \((\beta_n\ ;\ n\in{\mathbb N})\), \(\beta_n> 0, \forall n\), et deux nombres \(\lambda \in {\mathbb R},\ \delta\in {\mathbb R}_+^{\star}\) satisfaisant la relation :

\[ \lim_{n\rightarrow +\infty} F^n(\alpha_n+t\ \beta_n)=\exp(-\exp(-\frac{t-\lambda}{\delta})). \]

Alors :

\[ \lim_{n\rightarrow +\infty} {\cal L}(\frac{X_{(n)}-\alpha_n}{\beta_n})={\cal GU}(\lambda\ ;\ \delta). \]

Remarque 2. Nous avons une propriété analogue avec \({\cal L}(-X)\) et \({\cal L}(X_{(1)})={\cal L}(\displaystyle \min_{i=1}^n X_i)\).

Références. Des détails sur ces lois sont donnés dans les travaux de E. J. Gumbel (1937) et (2004) et de B. F. Kimball (1955).

Haut de la page.

4. Lois théoriques usuelles.

4. Lois théoriques usuelles.

4.9. Lois de Gumbel.