4.0. Introduction aux lois usuelles.
4.1. Lois indicatrices et associées.
4.2. Lois de Poisson.
4.3. Lois uniformes discrètes.
4.4. Lois Normales et associées.
4.5. Lois Gamma.
4.6. Lois Bêta.
4.7. Lois de Weibull.
4.8. Lois de Pareto.
4.9. Lois de Gumbel.
4.10. Lois de Cauchy.
4.11. Lois uniformes continues.
4.12. Famille exponentielle. \(\ast\)
4.13. Lois empiriques.
4.14. Lois associées à la Statistique d’ordre. \(\ast\)
Références bibliographiques.
Notations.
Commandes de R.
Index alphabétique.
Index des Mathématiciens - Statisticiens.
© Photis NOBELIS, 2009 à
.
Ancien Maître de Conférences en Statistique de l'Université Louis Pasteur de Strasbourg.
Je vous remercie de me signaler toutes mes omissions, erreurs, propositions d’amélioration du site, etc. Dans la mesure du possible, si mon temps le permet, je répondrai également à vos questions.
Nous présentons la famille de lois Gamma ou d’Euler très utiles pour les propriétés de décroissance rapide de leur fonction de survie. Pour cela nous introduisons une fonction spéciale.
Définition 1. Nous appelons fonction Gamma la fonction définie par :
\[ \Gamma(\alpha)=\int_0^{+\infty}t^{\alpha-1}e^{-t}dt,\quad \forall \alpha\in{\mathbb R}_+^{\star}. \]Propriété 1. La fonction Gamma satisfait aux relations suivantes :
\[ \Gamma(\alpha+1)=\alpha\Gamma(\alpha),\quad \forall \alpha\in{\mathbb R}_+^{\star},\qquad \Gamma(n+1)=n!,\quad \forall n\in{\mathbb N},\qquad \Gamma(0,5)=\sqrt{\pi}. \]Remarque 1. La fonction Gamma est une généralisation directe de la notion de factorielle pour des nombres réels non entiers. Le logiciel R permet d’obtenir des valeurs de gamma :
gamma(4) ; réponse : 6.
gamma(0.5) ; réponse : 1.772454.
gamma(2.18) ; réponse : 1.089999.
Définition 2. Une v.a. \(X\) suit une loi Gamma, ou eulerienne de paramètres \(\alpha,\ \beta \in {\mathbb R}_+^{\star}\) si elle admet pour densité de probabilité la fonction :
\[ f_X(t) =\cases{ \frac{\beta^{\alpha}}{\Gamma(\alpha)}t^{\alpha-1}e^{-\beta t} & \( {\it si}\ 0< t\),\cr 0 & \( {\it si}\ t\leq 0\) } \]Ceci est noté \({\cal L}(X)={\cal GA}(\alpha\ ;\ \beta)\). La loi \({\cal GA}(1\ ;\ \beta)={\cal E}(\beta)\) est appelée loi Exponentielle de paramètre \(\beta\).
Modélisation. La loi Gamma peut décrire des phénomènes de durée de vie, en assurance pour l’étude du temps écoulé entre deux sinistres dans des portefeuilles à risques hétérogènes ou encore pour prendre en compte cette hétérogénéité. En général pour des distributions fortement asymétriques avec une décroissance rapide en queue de distribution, une loi Gamma peut être un bon modèle.
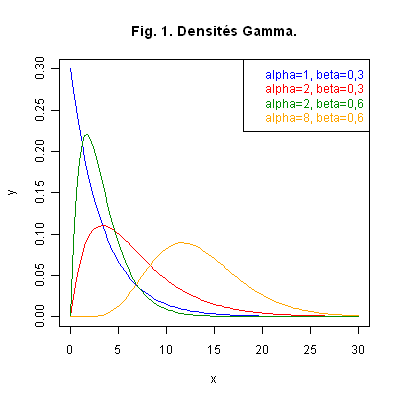
Graphique 1. La Fig. 1 ci-dessous représente les courbes des densités de loi Gamma \({\cal GA}(1\ ;\ 0,3)\), \({\cal GA}(2\ ;\ 0,3)\), \({\cal GA}(2\ ;\ 0,6)\) et \({\cal GA}(8\ ;\ 0,6)\). Nous voyons évoluer l’allure de la densité en fonction des paramètres.
Calculs avec R. A la base, les commandes comprennent l’expression «gamma» précédée d’une lettre spécifiant le calcul à réaliser. Les options shape et rate de la commande donnent respectivement \(\alpha\) et \(\beta\). Par exemple, si \({\cal L}(X)={\cal GA}(2\ ;\ 0,3)\), alors \(f_X(4)\) se détermine avec la commande :
dgamma(4, shape=2, rate=.3) ; réponse : 0.1084299.
Pour calculer \(P(X\leq 4)\) nous utilisons la commande :
pgamma(4, shape=2, rate=.3) ; réponse : 0.3373727.
Pour calculer le quantile d’ordre 0,95 nous utilisons la commande :
qgamma(0.95, shape=2, rate=.3) ; réponse : 15.81288.
Il est possible de réaliser des simulations d’observations d’une loi Gamma avec la commande : rgamma et les paramètres souhaités.
Propriété 2. Si \({\cal L}(X)={\cal GA}(\alpha\ ;\ \beta)\) alors :
\[ {\mathbb E}\lbrack X \rbrack = \frac{\alpha}{\beta},\quad \sigma^2\lbrack X\rbrack =\frac{\alpha}{\beta^2},\quad Mo\lbrack X\rbrack=\frac{\alpha-1}{\beta}, \quad {\it pour}\quad \alpha >1, \quad \gamma_1\lbrack X\rbrack = \frac{2}{\sqrt{\alpha}}\quad {\it et}\quad \gamma_2\lbrack X\rbrack = \frac{3(\alpha+2)}{\alpha}. \]De plus la fonction génératrice des moments est \( g_X(t)= (1-\dfrac{t}{\beta})^{-\alpha}\), pour tout \(t< \beta.\)
Remarque 2. A l’exception des lois exponentielles, il n’existe pas d’expression explicite pour la fonction de répartition \( F_X(t)= P(X\leq t)\), la fonction de survie \( S_X(t)= 1-F_X(t)=P(t< X)\), la médiane et les quantiles d’une loi Gamma. Il faut utiliser les commandes de R ci-dessus pour les évaluer dans chaque cas.
Propriété 3. La loi \({\cal GA}(\displaystyle\frac{n}{2}\ ;\ \frac{1}{2})=\chi^2_n\) est appelée loi du khi-deux.
Propriété 4. Soit \( X_i,\ i=1,\ \cdots,\ n,\) des variables aléatoires indépendantes de loi \({\cal GA}(\alpha_i\ ;\ \beta)\) respectivement. Alors pour tout nombre \(c \in {\mathbb R}_+^{\star}\) nous avons :
\[ {\cal L}(c(X_1+\cdots+X_n))={\cal GA}(\alpha_1+\cdots+\alpha_n\ ; \ \frac{\beta}{c}). \]Les lois Gamma sont liées aux lois de Poisson (cf. Propriété 7), aux lois de Pareto (cf. Propriété 5) et aux lois de Weibull (cf. Propriété 2). Les lois Exponentielles sont liées, quant à elles, aux lois de Gumbel (cf. Propriété 2).
Haut de la page.