4.0. Introduction aux lois usuelles.
4.1. Lois indicatrices et associées.
4.2. Lois de Poisson.
4.3. Lois uniformes discrètes.
4.4. Lois Normales et associées.
4.5. Lois Gamma.
4.6. Lois Bêta.
4.7. Lois de Weibull.
4.8. Lois de Pareto.
4.9. Lois de Gumbel.
4.10. Lois de Cauchy.
4.11. Lois uniformes continues.
4.12. Famille exponentielle. \(\ast\)
4.13. Lois empiriques.
4.14. Lois associées à la Statistique d’ordre. \(\ast\)
Références bibliographiques.
Notations.
Commandes de R.
Index alphabétique.
Index des Mathématiciens - Statisticiens.
© Photis NOBELIS, 2009 à
.
Ancien Maître de Conférences en Statistique de l'Université Louis Pasteur de Strasbourg.
Je vous remercie de me signaler toutes mes omissions, erreurs, propositions d’amélioration du site, etc. Dans la mesure du possible, si mon temps le permet, je répondrai également à vos questions.
Les lois que nous présentons ici ont mentionnées en premier lieu par Fréchet puis étudiées par Weibull dont elles prirent le nom. Elles sont très utiles en contrôle de la qualité.
Définition 1. Une v.a. continue \(X\) suit une loi de Weibull, de paramètres \(\alpha, \beta \in {\mathbb R}_+^{\star}\) si elle admet pour densité de probabilité la fonction :
\[ f_X(t)=\cases{ \beta \alpha t^{\alpha-1}e^{-\beta t^{\alpha}} &\( {\it si}\quad 0< t\),\cr 0 & \({\it si}\quad t\leq 0\). } \]Cela est noté \({\cal L}(X)={\cal W}(\alpha\ ;\ \beta)\).
Modélisation. La loi de Weibull peut décrire des phénomènes de durée de vie d’un matériel, d’un composant ou d’un système. Elle peut également modéliser le temps d’attente de la première panne, ou encore le temps écoulé entre deux pannes consécutives. Donc ce sont des lois d’une importance capitale en contrôle de la qualité et surtout en fiabilité.
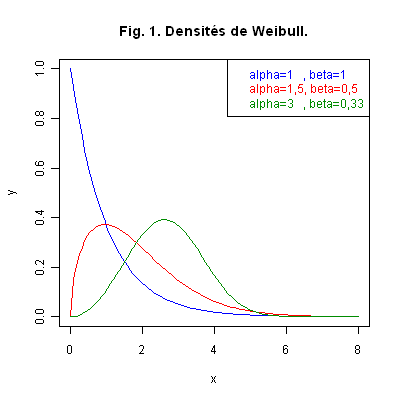
Graphique 1. La Fig. 1 ci-dessous représente les courbes des densités de loi Weibull \({\cal W}(1\ ;\ 1)\), \({\cal W}(1,5\ ;\ 0,5)\) et \({\cal W}(3\ ;\ 0,33)\). Nous voyons évoluer l’allure de la densité en fonction des paramètres.
Calculs avec R. Si \({\cal L}(X)={\cal W}(1,5\ ;\ 0,5)\), alors \(f_X(3)\) se détermine avec la commande :
dweibull(3,shape=1.5,scale=2) ; réponse : 0.1463043.
Pour calculer \(P(X\leq 3)\) nous utilisons la commande :
pweibull(3,shape=1.5,scale=2,lower.tail=T) ; réponse : 0.8407241.
Pour calculer la médiane nous utilisons la commande :
qweibull(0.5,shape=1.5,scale=2,lower.tail=T) ; réponse : 1.566440.
Il est possible de réaliser des simulations d’observations d’une loi Weibull avec la commande : rweibull et les paramètres souhaités.
Propriété 1. Si \({\cal L}(X)={\cal W}(\alpha\ ;\ \beta)\) alors :
\[ {\mathbb E}\lbrack X \rbrack = \frac{\Gamma(1+\frac{1}{\alpha})}{\beta^{\frac{1}{\alpha}}},\quad \sigma^2\lbrack X\rbrack =\frac{1}{\beta^{\frac{2}{\alpha}}} (\Gamma(\frac{2}{\alpha}+1)-\Gamma^2(\frac{1}{\alpha})),\quad Mo\lbrack X\rbrack=(\frac{\alpha-1}{\alpha\beta})^{\frac{1}{\alpha}}\quad {\it et}\quad Me\lbrack X\rbrack = (\frac{\ln{(2)}}{\beta})^{\frac{1}{\alpha}}. \]De plus la fonction de répartition \( F_X(t)\) et la fonction de survie \(S_X(t)\) sont données par :
\[ F_X(t)=P(X\leq t)=1-\exp{(-\beta t^{\alpha})}, \quad S_X(t)=P(t<X)=\exp{(-\beta t^{\alpha})},\quad \forall t\in {\mathbb R_+^{\star}}. \]Les lois de Weibull sont liées aux lois Gamma de la manière suivante.
Propriété 2. Si \({\cal L}(X)={\cal W}(\alpha\ ;\ \beta)\) alors \({\cal L}(X^{\alpha})={\cal GA}(1, \beta)={\cal E}(\beta)\). Si \({\cal L}(Y)={\cal GA}(1, \beta)={\cal E}(\beta)\) alors, pour tout \(\alpha\in {\mathbb R}_+^{\star}\), \({\cal L}(Y^{\frac{1}{\alpha}})={\cal W}(\alpha\ ;\ \beta)\).
Haut de la page.