4.0. Introduction aux lois usuelles.
4.1. Lois indicatrices et associées.
4.2. Lois de Poisson.
4.3. Lois uniformes discrètes.
4.4. Lois Normales et associées.
4.5. Lois Gamma.
4.6. Lois Bêta.
4.7. Lois de Weibull.
4.8. Lois de Pareto.
4.9. Lois de Gumbel.
4.10. Lois de Cauchy.
4.11. Lois uniformes continues.
4.12. Famille exponentielle. \(\ast\)
4.13. Lois empiriques.
4.14. Lois associées à la Statistique d’ordre. \(\ast\)
Références bibliographiques.
Notations.
Commandes de R.
Index alphabétique.
Index des Mathématiciens - Statisticiens.
© Photis NOBELIS, 2009 à
.
Ancien Maître de Conférences en Statistique de l'Université Louis Pasteur de Strasbourg.
Je vous remercie de me signaler toutes mes omissions, erreurs, propositions d’amélioration du site, etc. Dans la mesure du possible, si mon temps le permet, je répondrai également à vos questions.
Les lois de Cauchy sont intéressantes par les aspects théoriques particuliers qu’elles présentent.
Définition 1. v.a. continue \(X\) suit une loi de Cauchy, de paramètres \(\alpha \in {\mathbb R}_+^{\star}\) (paramètre d’échelle) et \(x_0 \in {\mathbb R}\) (paramètre de position) si elle admet pour densité de probabilité la fonction :
\[ f_X(t) =\frac{1}{\pi}\frac{\alpha}{\alpha^2 +(t-x_0)^2},\quad t\in {\mathbb R}. \]Ceci est noté \({\cal L}(X)={\cal CA}(x_0\ ;\ \alpha)\).
Modélisation. La loi de Cauchy présente la particularité de n’avoir aucun moment. La loi \({\cal L}(X)={\cal CA}(0\ ;\ 1)\) correspond à la distribution de la tangente de l’angle formé par un vecteur de \({\mathbb R}^2\) et l’axe des abscisses lorsque les coordonnées de ce vecteur sont distribuées, indépendamment l’une de l’autre, selon une loi \({\cal N}(0\ ;\ 1)\). De manière précise nous avons le résultat suivant.
Propriété 1. Si deux v.a. \(X\) et \(Y\) sont indépendantes et de loi \({\cal N}(0\ ;\ 1)\) alors :
\[ {\cal L}(\frac{X}{Y})={\cal CA}(0\ ;\ 1). \]Graphique 1. La Fig. 1 ci-dessous représente les courbes des densités de loi Cauchy \({\cal CA}(0\ ;\ 1)\), \({\cal CA}(1\ ;\ 1)\), et \({\cal CA}(1,5\ ;\ 2)\). Nous voyons évoluer l’allure de la densité en fonction des paramètres.
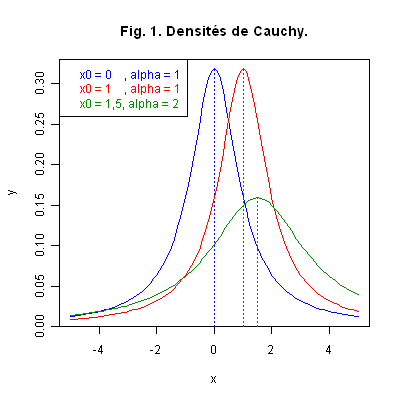
Nous constatons que la courbe représentative d’une densité de Cauchy est symétrique par rapport à une droite verticale au point \(x_0\), qu’elle ressemble à une cloche comme une loi Normale, sans en être vraiment une ; elle est bien plus aplatie.
Calculs avec R. A la base, les commandes comprennent l’expression «cauchy» précédée d’une lettre spécifiant le calcul à réaliser. Les options «location» et «scale» de la commande correspondent respectivement à \(x_0\) et \(\alpha\). Par exemple, si \({\cal L}(X)={\cal CA}(1\ ;\ 1)\), alors \(f_X(2)\) se détermine avec la commande :
dcauchy(2, location=1, scale=1) ; réponse : 0.1591549.
Pour calculer \(P(X\leq 2,5)\) nous utilisons la commande :
pcauchy(2.5, location=1, scale=1, lower.tail=TRUE) ; réponse : 0.812833.
Pour calculer le troisième quartile nous utilisons la commande :
qcauchy(.75, location=1, scale=1, lower.tail=TRUE) ; réponse : 2.
Il est possible de réaliser des simulations d’observations d’une loi de Cauchy avec la commande rcauchy et les paramètres souhaités.
Propriété 2. Si \({\cal L}(X)={\cal CA}(x_0\ ;\ \alpha)\) alors la v.a. \(X\) ne possède ni moyenne théorique ni, a fortiori, variance théorique. Elle n’admet pas non plus de fonction génératrice des moments. Sa fonction de répartition est donnée par :
\[ F_X(t)=\frac{1}{2}+\frac{1}{\pi}Arctg(\frac{t-x_0}{\alpha}). \]Propriété 3. Si \({\cal L}(X)={\cal CA}(x_0\ ;\ \alpha)\) alors nous avons les résultats :
\[ Mo\lbrack X\rbrack=Me\lbrack X\rbrack=x_0,\quad Q_{0,25}\lbrack X\rbrack=x_0-\alpha,\quad Q_{0,75}\lbrack X\rbrack=x_0+\alpha\quad {\rm et}\quad IQR\lbrack X\rbrack=2\alpha. \]Cette dernière propriété implique que pour représenter numériquement une variable distribuée selon une loi de Cauchy, ce sont ces quantités qu’il faudra utiliser.
Haut de la page.