Lois uniformes continues.

4.11. Lois uniformes continues.

Les lois uniformes continues sont très utiles de par la facilité des calculs qu’elles permettent et pour leur utilisation dans les simulations.

Définition 1. Une v.a. \(X\) suit une loi de Uniforme continue de paramètres \(\theta_1,\ \theta_2 \in {\mathbb R}\), avec \(\theta_1 < \theta_2\), si elle admet pour densité de probabilité la fonction :

\[ f_X(t) =\frac{1}{\theta_2-\theta_1}I_{\rbrack \theta_1\ ;\ \theta_2\lbrack}(t)=\cases{ 0 \quad {\it si} & \(t \notin \rbrack \theta_1\ ;\ \theta_2\lbrack\),\cr \displaystyle\frac{1}{\theta_2-\theta_1} \quad {\it si} & \( t \in \rbrack \theta_1\ ;\ \theta_2\lbrack\). } \]

Ceci est noté \({\cal L}(X)={\cal U}(\rbrack \theta_1\ ;\ \theta_2\lbrack)\).

Modélisation. La loi Uniforme, comme son nom l’indique, peut représenter la distribution des réalisations d’une telle v.a. sur toute la longueur d’un intervalle, de temps par exemple, lorsque celles-ci sont uniformément réparties.

Propriété 1. Si \({\cal L}(X)={\cal U}(\rbrack \theta_1\ ;\ \theta_2\lbrack)\) sa f.r. est donnée par :

\[ F_X(t)=\frac{t-\theta_1}{\theta_2-\theta_1}I_{\rbrack \theta_1\ ;\ \theta_2\lbrack}(t)+I_{\lbrack \theta_2\ ;\ +\infty \lbrack}(t)=\cases{ 0 \quad {\it si} & \( t \leq \theta_1\) , \cr \displaystyle\frac{t-\theta_1}{\theta_2-\theta_1} \quad {\it si} &\( \theta_1 < t < \theta_2\),\cr 1 \quad {\it si} &\( \theta_2 \leq t\). } \]

Graphique 1. A titre d’exemple, la Fig. 1 ci-dessous représente la courbe de la f.r. de la loi \({\cal U}(\rbrack 1,5\ ;\ 3,5\lbrack)\).

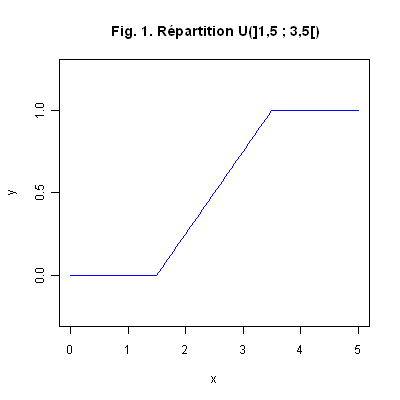
Remarquons que cette f.r. est continue mais n’est pas dérivable aux points \(x=1,5\) et \(x=3,5\).

Calculs avec R. Si \({\cal L}(X)={\cal U}(\rbrack 1,5\ ;\ 3,5\lbrack)\), alors :

le nombre \(f_X(t)\) se détermine avec dunif(t,min=1.5,max=3.5),

le nombre \(F_X(t)=P(X\leq t)\) se détermine avec punif(t,min=1.5,max=3.5,lower.tail=TRUE),

le quantile d’ordre q se détermine avec qunif(q,min=1.5,max=3.5,lower.tail=TRUE).

Il est possible de réaliser des simulations d’observations d’une loi Uniforme avec la commande runif et les paramètres souhaités.

Propriété 2. Si \({\cal L}(X)={\cal U}(\rbrack \theta_1\ ;\ \theta_2\lbrack)\) alors :

\[ {\mathbb E}\lbrack X \rbrack = Me\lbrack X\rbrack = \frac{\theta_1+\theta_2}{2},\quad \sigma^2\lbrack X\rbrack =\frac{(\theta_2-\theta_1)^2}{12} \]

\[ Q_{0,25}\lbrack X\rbrack=\theta_1+\frac{\theta_2-\theta_1}{4},\quad Q_{0,75}\lbrack X\rbrack=\theta_1+3\frac{\theta_2-\theta_1}{4},\quad {\rm et}\quad IQR\lbrack X\rbrack=\frac{\theta_2-\theta_1}{2}. \]

Propriété 3. Soit \(Y\) une v.a. de loi quelconque, de f.r. \(F_Y(t)\) inversible. Alors la v.a. \(X=F_y(Y)\) est de loi \({\cal U}(\rbrack 0\ ;\ 1\lbrack)\).

Cette propriété permet de réaliser des simulations de diverses lois. En effet il existe plusieurs programmes qui permettent de simuler une observation \(x\) de la loi \({\cal U}(\rbrack 0\ ;\ 1\lbrack)\). Puis, en posant \(y=F_Y^{-1}(x)\), ou en résolvant l’équation \(x=F_Y(y)\), nous obtenons \(y\) une observation simulée de \({\cal L}(Y)\).

Exemple 1. Supposons que nous souhaitons simuler une observation \(y\) de \(Y\), v.a. suivant une loi de Bernoulli \({\cal L}(X)={\cal B}(1\ ;\ p)\). Soit \(x\) une simulation de \({\cal U}(\rbrack 0\ ;\ 1\lbrack)\). Alors en posant :

\[ y =\cases{ 0 \quad {\rm si} & \( x < 1-p\),\cr 1 \quad {\rm si} & \( 1-p \leq x\), } \]

nous obtenons une simulation de \({\cal L}(Y)={\cal B}(1\ ;\ p)\).

Exemple 2. Supposons que nous souhaitons simuler une observation \(y\) de \(Y\), v.a. suivant une loi Exponentielle \({\cal GA}(1\ ;\ \beta)={\cal E}(\beta)\). Sa f.r. est \(F_Y(y)=1-\exp{(-\beta y)}\). Soit \(x\) une simulation de \({\cal U}(\rbrack 0\ ;\ 1\lbrack)\). Alors en posant :

\[ y =\frac{1}{\beta}\ln{(\frac{1}{1-x})} \]

nous obtenons une simulation de \(Y\), avec \({\cal L}(Y)={\cal E}(\beta)\).

Haut de la page.

4. Lois théoriques usuelles.

4. Lois théoriques usuelles.

4.11. Lois uniformes continues.