Lois Log-Normales.

4.4.3. Lois Log-Normales.

Les lois Log-Normales, dérivées directement des lois Normales, sont très fréquentes dans la nature et dans diverses activités humaines.

Définition 1. Une v.a. continue \(X\) suit une loi de Log-Normale, de paramètres \(x_0,\ \mu\in {\mathbb R}\) et \(\sigma \in {\mathbb R}_+^{\star}\) si \({\cal L}(\ln(X-x_0))={\cal N}(\mu\ ;\ \sigma^2)\). Elle admet alors pour densité de probabilité la fonction :

\[ f_X(t) =\frac{1}{(t-x_0)\sigma \sqrt{2\pi}}\exp\left(\displaystyle - \frac{1}{2\sigma^2} (\ln(t-x_0)-\mu)^2\right)I_{\rbrack x_0\ ;\ +\infty\lbrack}(t),\quad t\in {\mathbb R}. \]

Cela est noté \({\cal L}(X)=Log-{\cal N}(x_0\ ;\ \mu\ ;\ \sigma^2)\).

Modélisation. Ces lois sont utilisées dans le même cadre que les lois normales, mais lorsque les mesures ou observations sont le résultat d’un effet multiplicatif d’un très grand nombre d’autres variables, indépendantes entre elles et individuellement négligeables. Outre les applications en Biologie dans l’effet multiplicatif d’une dose d’une substance, nous avons également des applications en assurance où la loi Log-Normale peut représenter la distribution des coûts de sinistres. Plus généralement, lorsque la distribution des observations est très asymétrique, il faudrait tenter d’ajuster une loi Log-Normale.

Graphique 1. La Fig. 1 ci-dessous représente les courbes de plusieurs densités de lois Log-Normales de paramètres différents.

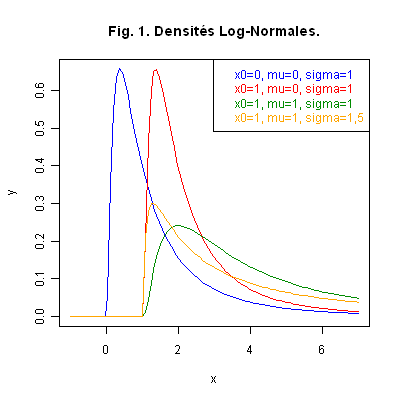
Propriété 1. Si \({\cal L}(X)=Log-{\cal N}(x_0\ ;\ \mu\ ;\ \sigma^2)\) alors :

\[ Mo\lbrack X\rbrack=x_0+e^{\mu-\sigma^2},\quad Me\lbrack X\rbrack = x_0+e^{\mu},\quad {\mathbb E}\lbrack X \rbrack = x_0+e^{\mu+\frac{\sigma^2}{2}},\quad \sigma^2\lbrack X\rbrack =e^{2\mu+\sigma^2}\left(e^{\sigma^2}-1\right). \]

De plus

\[ \gamma_1\lbrack X\rbrack =\left(e^{\sigma^2}+2\right)\sqrt{e^{\sigma^2}-1} \quad {\rm et}\quad \gamma_2\lbrack X\rbrack = e^{4\sigma^2}+2e^{3\sigma^2}+3e^{2\sigma^2}-6. \]

Remarque 1. Nous constatons la forte asymétrie droite.

Calculs avec R. Si \({\cal L}(X)=Log-{\cal N}(2\ ;\ 1\ ;\ 1,5^2)\), alors nous avons :

\(f_X(t)\) se calcule avec dlnorm(t-2,meanlog=1,sdlog=1.5),

\(F_X(t)=P(X\leq t)\) se calcule avec plnorm(t-2,meanlog=1,sdlog=1.5,lower.tail=TRUE),

le quantile d’ordre p se détermine avec qlnorm(p,meanlog=1,sdlog=1.5,lower.tail=TRUE)+2.

Il est possible de réaliser des simulations d’observations d’une loi Log-Normale avec la commande rlnorm et les paramètres souhaités.

Haut de la page.

4. Lois théoriques usuelles.

4. Lois théoriques usuelles.

4.4.3. Lois Log-Normales.