Tests sur une proprtion théorique - alternatives bilatérales.

7.5.4.b. Tests asymptotiques sur une proportion théorique - Contre-hypothèses bilatérales.

Nous présentons des tests asymptotiques des Alternatives 2 et Alternatives 3 pour une proportion théorique. Les tests exacts sont décrits dans l’étude des paramètres d’une loi de Bernoulli. Comme pour l’estimation d’une proportion théorique, nous utilisons des méthodes asymptotiques générales, forcément approximatimatives. Les risques et valeurs critiques sont établis pour \(n\rightarrow+\infty\), il est donc souhaitable d’avoir au moins \(50\) observations. Les résultats devront être interprétés avec réserve. Dans chaque cas nous donnons un exemple.

Dans une population, nous considérons la proportion \(p\in \rbrack 0\ ;\ 1\lbrack\), inconnue, d’unités qui possèdent un caractère donné \({\cal C}\). Pour l’étude de la présence de \({\cal C}\), nous savons que le modèle le plus adapté est celui de Bernoulli \({\cal B}(1\ ;\ p)\). Si \(X\) est la v.a. indicatrice de la présence de \({\cal C}\) alors \(P(X=0)=1-p\), \(P(X=1)=p\), \({\mathbb E}\lbrack X\rbrack=p\) et \({\mathbb V}ar\lbrack X\rbrack=p(1-p)\). Soit \(X_{\bullet}=(X_1,\ \cdots,\ X_n)\) un \(n-\)échantillon de \(X\). Alors la somme \(\sum_{j=1}^nX_j\) correspond à l’effectif des unités de l’échantillon possédant le caractère \({\cal C}\) (nombre de «un») et la statistique moyenne empirique \(\overline{X}\) est la proportion ou encore la fréquence de \({\cal C}\) dans l’échantillon. C’est pour quoi nous notons \(\overline{X}=F_{\cal C}(X_{\bullet})=F_{\cal C}\) et une réalisation \(F_{\cal C}=f_{\cal C}\). Nous savons que \({\mathbb E}\lbrack F_{\cal C}\rbrack=p\) et que \({\mathbb V}ar\lbrack F_{\cal C}\rbrack=\dfrac{p(1-p)}{n}\).

Propriété 1. Nous avons les résultats suivants :

\(F_{\cal C}\overset{P}{\underset{n\rightarrow+\infty}\longrightarrow}p\).
\(\displaystyle\lim_{n\rightarrow +\infty} {\cal L}_p\left(\sqrt{n}\frac{F_{\cal C}-p}{\sqrt{p(1-p)}}\right)={\cal N}(0\ ;\ 1)\), c’est-à-dire \(\displaystyle \lim_{n\rightarrow +\infty}P_p\left(\sqrt{n}\frac{F_{\cal C}-p}{\sqrt{p(1-p)}}\leq t\right)=\Phi(t),\ \forall t\in {\mathbb R}\).

Nous avons noté \({\cal N}(0\ ;\ 1)\) la loi Normale Standard et \(\Phi\) sa f.r..

Ces résultats sont fondés sur la loi Faible des Grands Nombres et le T.L.C..\(\ \square\)

Alternative 2.

Soit \(p_0\in\rbrack 0\ ;\ 1\lbrack\) donné et \(\alpha\in \rbrack 0\ ;\ 1\lbrack\) un seuil fixé. Pour tester l’alternative :

\({\cal H}_0^{(2)}=\lbrace p = p_0\rbrace\quad\) contre \(\quad{\cal H}_1^{(2)}=\lbrace p \not= p_0\rbrace\),

ainsi que les autres Alternatives 2 associées, nous considérons le test asymptotique \(\psi^{(2)}_{\infty}(x_{\bullet})=1-I_{\lbrack c_1\ ;\ c_2\rbrack}(f_{\cal C})\), avec \(c_1=c_{1,2}=p_0-q_{1-\frac{\alpha}{2}}\sqrt{\dfrac{p_0(1-p_0)}{n}}\) et \(c_2=c_{2,2}=p_0+q_{1-\frac{\alpha}{2}}\sqrt{\dfrac{p_0(1-p_0)}{n}}\) ; le nombre \(q_{1-\frac{\alpha}{2}}\) est le quantile d’ordre \(1-\dfrac{\alpha}{2}\) de la loi \({\cal N}(0\ ;\ 1)\). Ainsi :

si \( f_{\cal C}\notin \lbrack c_1\ ;\ c_2\rbrack\), alors nous décidons «\({\cal H}_1^{(2)}\) est vraie» ;
si \(f_{\cal C} \in \lbrack c_1\ ;\ c_2\rbrack\), alors nous décidons «\({\cal H}_0^{(2)}\) est vraie».

Conditions 2. Pour avoir une cohérence sur les valeurs critiques, nous admettons que la taille de l’échantillon a été fixée telle que :

\(\max\left(7\ ;\ q_{1-\frac{\alpha}{2}}\sqrt{\dfrac{p_0}{1-p_0}}\ ;\ q_{1-\frac{\alpha}{2}}\sqrt{\dfrac{1-p_0}{p_0}}\right) < \sqrt{n}\).

La première condition \(50 \leq n\) nous permet d’envisager l’approximation de le loi de la fréquence \(F_{\cal C}\) par une loi Normale. La deuxième condition \(q_{1-\frac{\alpha}{2}}\sqrt{\dfrac{p_0}{1-p_0}} <\sqrt{n}\) implique \(c_2 < 1\). La troisième condition \(q_{1-\frac{\alpha}{2}}\sqrt{\dfrac{1-p_0}{p_0}} <\sqrt{n}\) nous donne \(0 < c_1\). Enfin la condition \(0< \alpha < 1\) implique \(c_1<c_2\). Nous avons ainsi une cohérence pour le test.

Remarque 1. Si pour l’utilisateur décider à tort que la proportion de la population qui possède le caractère \({\cal C}\) n’est pas égale à une valeur fixée \(p_0\) a les conséquences les plus défavorables, c’est sur ce test \(\psi^{(2)}_{\infty}(F_{\cal C})\) qu’il doit fonder sa démarche.

Remarque 2. Notons qu’il n’existe pas de test pour l’alternative :

\({\cal H}_0=\lbrace p\not= p_0\rbrace\ \) contre \(\ {\cal H}_1=\lbrace p = p_0\rbrace\quad \).

Mais nous pouvons utiliser le test \(\psi^{(4)}_{\infty}\) pour l’Alternative 4 :

\({\cal H}_0^{(4)}=\lbrace p\notin\lbrack p_1\ ; p_2\rbrack\rbrace\ \) contre \(\ {\cal H}_1^{(4)}=\lbrace p \in\lbrack p_1\ ; p_2\rbrack\rbrace\quad \).

Lorsque pour l’Alternative 3 :

\({\cal H}_0^{(3)}=\lbrace p\in\lbrack p_1\ ; p_2\rbrack\rbrace\ \) contre \(\ {\cal H}_1^{(3)}=\lbrace p \notin\lbrack p_1\ ; p_2\rbrack\rbrace\quad \),

\(p_1, p_2\rightarrow p_0\), alors le test \(\psi^{(3)}_{\infty}\), qui sera étudié ci-après, tend vers \(\psi^{(2)}_{\infty}\) avec le même seuil.

Propriété 2. Le test \(\psi^{(2)}_{\infty}\) satisfait à :

\(\displaystyle\lim_{n\rightarrow +\infty}{\mathbb E}_{p_0}\lbrack\psi^{(2)}_{\infty}(X_{\bullet})\rbrack=\alpha\) ; le test est asymptotiquement de seuil \(\alpha\).
Pour tout \(p\not=p_0\ ,\ \alpha\leq\displaystyle\lim_{n\rightarrow +\infty} pu_{\psi^{(2)}_{\infty}}(p)\) ; le test est asymptotiquement sans biais à ce seuil.
Pour tout \(p\), une approximation de la fonction puissance asymptotique est donnée par :
\(pu_{\psi^{(2)}_{\infty}}(p)\approx 1-\Phi\left(\sqrt{n}\dfrac{p_0-p}{\sqrt{p(1-p)}}+q_{1-\frac{\alpha}{2}}\sqrt{\dfrac{p_0(1-p_0)}{p(1-p)}}\right)+\)
\(\Phi\left(\sqrt{n}\dfrac{p_0-p}{\sqrt{p(1-p)}}-q_{1-\frac{\alpha}{2}}\sqrt{\dfrac{p_0(1-p_0)}{p(1-p)}}\right)\)

La Propriété 1.ii. et des calculs simples sur la f.r. de la loi Normale Standard, nous donnent ces résultats.\(\ \square\)

Remarque 3. Si nous avons observé \(F_{\cal C}=f_{\cal C}\), une approximation de la puissance asymptotique a posteriori est :

\(pu_{\psi^{(2)}_{\infty}}(f_{\cal C})\approx 1-\Phi\left(\sqrt{n}\dfrac{p_0-f_{\cal C}}{\sqrt{f_{\cal C}(1-f_{\cal C})}}+q_{1-\frac{\alpha}{2}}\sqrt{\dfrac{p_0(1-p_0)}{f_{\cal C}(1-f_{\cal C})}}\right)+\)
\(\Phi\left(\sqrt{n}\dfrac{p_0-f_{\cal C}}{\sqrt{f_{\cal C}(1-f_{\cal C})}}-q_{1-\frac{\alpha}{2}}\sqrt{\dfrac{p_0(1-p_0)}{f_{\cal C}(1-f_{\cal C})}}\right)\)

Propriété 3. Si nous avons observé \(F_{\cal C}=f_{\cal C}\), la \(p-\)valeur du test est \(p_{val}=2\left(1-\Phi\left(\sqrt{n}\dfrac{\mid f_{\cal C}-p_0\mid}{\sqrt{p_0(1-p_0)}}\right)\right).\) Ainsi :

si \(p_{val} < \alpha\), nous décidons «\({\cal H}_1^{(2)}\) est vraie»
si \(\alpha \leq p_{val}\), nous décidons «\({\cal H}_0^{(2)}\) est vraie».

Pour le voir, il suffit de faire apparaître \(1-\dfrac{\alpha}{2}=\Phi(q_{1-\frac{\alpha}{2}})\) dans les inégalités ci-dessus et d’effectuer un calcul direct. \(\ \square\)

Remarque 4. Pour réaliser le test \(\psi^{(2)}_{\infty}\) nous avons créé dans R quatre procédures. Les deux premières Test2Asym1Prop et Test2Asym1Prop_Int qui permettent la réalisation du test 1a avec exécution non interactive et interactive, respectivement. Les deux dernières Puis2Asym1Prop et Puis2Asym1Prop_Int permettent le calcul d’une approximation de la fonction puissance asymptotique du test 2 avec exécution non interactive et interactive, respectivement.

Exemple 1. Un cabinet d’expertise met en place un contrôle statistique de conformité concernant les pièces d’un lot produit par une usine. Ce lot est conforme si exactement \(4 \%\) des pièces sont défectueuses. Nous admettons que la situation la plus défavorable pour le cabinet est celle de décider à tort que le lot n’est pas conforme. Donc nous nous proposons de tester l’alternative :

\({\cal H}_0^{(2)}=\lbrace p = 0,04\rbrace\quad\) contre \(\quad{\cal H}_1^{(2)}=\lbrace p \not= 0,04\rbrace\),

Nous constatons que, sur \(210\) pièces choisies au hasard dans le lot, il y a \(3\) pièces non conformes. Nous fixons un seuil à \(0,01\) et nous exécutons, après les avoir compilées («sourcée» dans R), les procédures de la Remarque 4 ci-dessus.

Test2Asym1Prop (3,210,0.04,0.01), réponse :
Test asymptotique de l'alternative : H_0^{(2)}={ p = 0.04 } contre H_1^{(2)}={ p ≠ 0.04 }.
Condition de cohérence du test : 169 .
Taille de l'échantillon : 210 ; nombre de «un» : 3 ; proportion observée : 0.01429 .
Seuil asymptotique du test : 0.01 ; valeurs critiques : 0.005168 et 0.07483 .

P-valeur du test 1a : 0.05722 .
Décision : «H_0^{(2)}={p = 0.04 } est vraie».

Approximation de la puissance a posteriori du test : 0.1328 .

La procédure interactive donne quant à elle :

Test2Asym1Prop_Int(), réponse :
Saisir le nombre de «un» : 3, réponse :
Saisir la taille de l’échantillon : 210, réponse :
Saisir la proportion P0 : .04, réponse :
Saisir seuil du test : .01, réponse :
les mêmes résultats que ceux de la procédure non interactive sont alors affichés.

Contrairement aux exemples des Alternatives 1a et Alternatives 1b, il a fallu augmenter la taille de l'échantillon parce que la première valeur critique était négative. La décision est «\({\cal H}_0^{(2)}\) est vraie». Le test n’est pas significatif. La puissance asymptotique a posteriori est relativement faible : 0,1328. La décision est risquée. Pour être plus sûrs il faudrait augmenter l’échantillonnage. Nous pouvons calculer une approximation de la puissance asymptotique pour les points \(p=0,01429\) et \(p=0.055\) par exemple. Nous exécutons, après les avoir compilées («sourcée» dans R), les procédures de la Remarque 4 ci-dessus.

Puis2Asym1Prop(210,0.04,0.01,0.01429), réponse : 0.1327
Puis2Asym1Prop(210,0.04,0.01,0.055), réponse : 0.1045.

La procédure interactive, par exemple, donne quant à elle :

Puis2Asym1Prop_Int(), réponse :
Saisir la taille de l’échantillon : 201, réponse :
Saisir la proportion P0 : .04, réponse :
Saisir seuil du test : .01, réponse :
Saisir le point P où calculer une approximation de la puissance asymptotique : 0.055, réponse : 0.1045 .

Nous pouvons également tracer le graphique d’une approximation de la fonction puissance asymptotique du test avec les commandes suivantes :

plot( function(P) Puis2Asym1Prop(210,0.04,0.01,P),.0,.08, xlab="p",
ylab="pu", ylim= c(0,0.6), main=Fig 1. Approximation de la puissance\n asymptotique du test 2.", col="green4");
x0=c(0.04,0.04,0.01429,0.01429,0.055,0.055); y0=c(0,0.01,0,0.1328,0,.1045);
x1=c(0.04,0,0.01429,0,0.055,0); y1=c(0.01,0.01,0.1328,0.1328,0.1045,0.1045);
segments(x0,y0,x1,y1, col="blue");
points( x=c(0.04,0.01429,0.055), y=c(0.01,0.1328,0.1045), col="red", pch='.', cex=8), réponse :

Approximation de la fonction puissance asymptotique du test 2.

Remarquons que le graphique a l’allure générale de la puissance des tests \(pu_{\psi^{(2)}_{\infty}}\), mais il comporte une asymétrie. Celle-ci est d’autant plus prononcée que \(p_0\) est éloigné de part et d’autre de \(0,5\). Nous avons marqué en rouge les points de coordonnées \((p_0\ ;\ \alpha)=(0,04\ ;\ 0,01)\), \((0,01429\ ;\ pu_{\psi^{(2)}_{\infty}}(0,01429))\approx(0,01429\ ;\ 0,1328)\) et \((0,055\ ;\ pu_{\psi^{(2)}_{\infty}}(0,055))\approx(0,055\ ;\ 0,1045)\). Nous constatons, entre autres, que le test est asymptotiquement de seuil \(0,01\) et sans biais. \(\ \square\)

Alternative 3.

Soit \(p_1, p_2\in\rbrack 0\ ;\ 1\lbrack,\ p_1 < p_2\) et \(\alpha\in \rbrack 0\ ;\ 1\lbrack\) un seuil fixé. Pour tester l’alternative :

\({\cal H}_0^{(3)}=\lbrace p\in\lbrack p_1\ ;\ p_2\rbrack\rbrace\quad\) contre \(\quad{\cal H}_1^{(3)}=\lbrace p\notin\lbrack p_1\ ;\ p_2\rbrack\rbrace\),

ainsi que toutes les Alternatives 3 associées, nous considérons le test asymptotique \(\psi^{(3)}_{\infty}(x_{\bullet})=1-I_{\lbrack c_1\ ;\ c_2\rbrack}(f_{\cal C})\) avec \(c_1=c_{1,3}=p_1-q_{1-\alpha}\sqrt{\dfrac{p_1(1-p_1)}{n}}\) et \(c_2=c_{2,3}=p_2+q_{1-\alpha}\sqrt{\dfrac{p_2(1-p_2)}{n}}\) ; le nombre \(q_{1-\alpha}\) est le quantile d’ordre \(1-\alpha\) de la loi \({\cal N}(0\ ;\ 1)\). Ainsi :

si \( f_{\cal C}\notin \lbrack c_1\ ;\ c_2\rbrack\), alors nous décidons «\({\cal H}_1^{(3)}\) est vraie» ;
si \(f_{\cal C} \in \lbrack c_1\ ;\ c_2\rbrack\), alors nous décidons «\({\cal H}_0^{(3)}\) est vraie».

Conditions 3. Pour avoir une cohérence sur les valeurs critiques, nous admettons que la taille de l’échantillon a été fixée telle que :

\(\max\left(7\ ;\ q_{1-\alpha}\sqrt{\dfrac{1-p_1}{p_1}}\ ;\ q_{1-\alpha}\sqrt{\dfrac{p_2}{1-p_2}}\ ;\ \dfrac{q_{\alpha}}{p_2-p_1}\sqrt{p_2(1-p_2)+p_1(1-p_1)}\right) < \sqrt{n}\).

La première condition \(50 \leq n\) nous permet d’envisager l’approximation de le loi de la fréquence \(F_{\cal C}\) par une loi Normale. La deuxième condition \(q_{1-\alpha}\sqrt{\dfrac{1-p_1}{p_1}} <\sqrt{n}\) implique \(0 < c_1\). La troisième condition \(q_{1-\alpha}\sqrt{\dfrac{p_2}{1-p_2}} <\sqrt{n}\) nous donne \(c_2 < 1\). Enfin la dernière condition implique \(c_1<c_2\). Nous avons ainsi une cohérence pour le test et ses valeurs critiques.

Remarque 5. Si pour l’utilisateur décider à tort que la proportion de la population qui possède le caractère \({\cal C}\) n’est pas dans un intervalle donné a les conséquences les plus défavorables, c’est sur ce test \(\psi^{(3)}_{\infty}(F_{\cal C})\) qu’il doit fonder sa démarche.

Remarque 6. Si \(p_1, p_2\rightarrow p_0\), l’alternative \({\cal H}_0^{(3)}\) contre \({\cal H}_1^{(3)}\) devient l’alternative \({\cal H}_0^{(2)}\) contre \({\cal H}_1^{(2)}\) et le test \(\psi^{(3)}_{\infty}\) tend vers le test \(\psi^{(2)}_{\infty}\) au même seuil. De plus si nous considérons les alternatives

\({\cal H}_0^{(3)}\) contre \(\ {\cal H}_1^{(3)}\) et \({\cal H}_0^{(4)}\) contre \({\cal H}_1^{(4)}\),

le test \(\psi^{(3)}_{\infty}\), au seuil \(\alpha\), et le test \(1-\psi^{(4)}_{\infty}\), au seuil \(1-\alpha\), sont identiques.

Propriété 4. Le test \(\psi^{(3)}_{\infty}\) satisfait à :

Pour tout \(p\in\lbrack p_1 ; p_2\rbrack\ \displaystyle\lim_{n\rightarrow +\infty}{\mathbb E}_{p}\lbrack\psi^{(3)}_{\infty}\rbrack\leq \displaystyle\lim_{n\rightarrow +\infty}{\mathbb E}_{p_1}\lbrack\psi^{(3)}_{\infty}\rbrack=\displaystyle\lim_{n\rightarrow +\infty}{\mathbb E}_{p_2}\lbrack\psi^{(3)}_{\infty}\rbrack=\alpha\) ; le test est asymptotiquement de seuil \(\alpha\).
Pour tout \(p\notin\lbrack p_1 ; p_2\rbrack,\ \alpha\leq\displaystyle\lim_{n\rightarrow +\infty} pu_{\psi^{(3)}_{\infty}}(p)\) ; le test est asymptotiquement sans biais à ce seuil.
Pour tout \(p\), une approximation de la fonction puissance asymptotique est donnée par :
\(pu_{\psi^{(3)}_{\infty}}(p)\approx 1-\Phi\left(\sqrt{n}\dfrac{p_2-p}{\sqrt{p(1-p)}}+q_{1-\alpha}\sqrt{\dfrac{p_2(1-p_2)}{p(1-p)}}\right)+\)
\(\Phi\left(\sqrt{n}\dfrac{p_1-p}{\sqrt{p(1-p)}}-q_{1-\alpha}\sqrt{\dfrac{p_1(1-p_1)}{p(1-p)}}\right)\)

La Propriété 1. et des calculs simples sur la f.r. de la loi Normale Standard, nous donnent ces résultats.\(\ \square\)

Remarque 7. Si nous avons observé \(F_{\cal C}=f_{\cal C}\), une approximation de la puissance asymptotique a posteriori est :

\(pu_{\psi^{(3)}_{\infty}}(f_{\cal C})\approx 1-\Phi\left(\sqrt{n}\dfrac{p_2-f_{\cal C}}{\sqrt{f_{\cal C}(1-f_{\cal C})}}+q_{1-\alpha}\sqrt{\dfrac{p_2(1-p_2)}{f_{\cal C}(1-f_{\cal C})}}\right)+\)
\(\Phi\left(\sqrt{n}\dfrac{p_1-f_{\cal C}}{\sqrt{f_{\cal C}(1-f_{\cal C})}}-q_{1-\alpha}\sqrt{\dfrac{p_1(1-p_1)}{f_{\cal C}(1-f_{\cal C})}}\right)\)

Propriété 5. Si nous avons observé \(F_{\cal C}=f_{\cal C}\), la \(p-\)valeur du test est

\(p_{val}=\min\left\lbrace\Phi\left(\sqrt{n}\dfrac{f_{\cal C}-p_1}{\sqrt{p_1(1-p_1)}}\right)\ ;\ \Phi\left(\sqrt{n}\dfrac{p_2-f_{\cal C}}{\sqrt{p_2(1-p_2)}}\right)\right\rbrace.\)

Ainsi :

si \(p_{val} < \alpha\), nous décidons «\({\cal H}_1^{(3)}\) est vraie»
si \(\alpha \leq p_{val}\), nous décidons «\({\cal H}_0^{(3)}\) est vraie».

Pour le voir, il suffit de faire apparaître \(1-\alpha=\Phi(q_{1-\alpha})\) dans les inégalités ci-dessus et d’effectuer un calcul direct. \(\ \square\)

Remarque 8. Pour réaliser le test \(\psi^{(3)}_{\infty}\) nous avons créé dans R quatre procédures. Les deux premières Test3Asym1Prop et Test3Asym1Prop_Int qui permettent la réalisation du test 3 avec exécution non interactive et interactive, respectivement. Les deux dernières Puis3Asym1Prop et Puis3Asym1Prop_Int permettent le calcul d’une approximation de la fonction puissance asymptotique du test 3 avec exécution non interactive et interactive, respectivement.

Exemple 2. Nous reprenons l’Exemple 1. Mais nous considérons, pour l’alternative, non plus une valeur \(p_0\), mais un intervalle \(\lbrack p_1 ; p_2\rbrack\). Un cabinet d’expertise met en place un contrôle statistique de conformité concernant les pièces d’un lot produit par une usine. Ce lot est conforme si la proportion théorique des pièces défectueuses est comprise entre \(3,5\%\) et \(4,5\%\). Nous admettons que la situation la plus défavorable pour le cabinet est celle de décider à tort que le lot n’est pas conforme. Donc nous nous proposons de tester l’alternative :

\({\cal H}_0^{(3)}=\lbrace p\in\lbrack 0,035\ ;\ 0,045\rbrack\rbrace\quad\) contre \(\quad{\cal H}_1^{(3)}=\lbrace p\notin\lbrack 0,035\ ;\ 0,045\rbrack\rbrace\),

Tes3Asym1Prop (3,210,.035,.045,.01), réponse :
Test asymptotique de l'alternative : H_0^{(3)}={ 0.035 ⩽ P ⩽ 0.045 } contre H_1^{(3)}={ P < 0.035 ou 0.045 < P}.
Condition de cohérence du test : 169 .
Taille de l'échantillon : 210 ; nombre de «un» : 3 ; proportion observée : 0.01429 .
Seuil asymptotique du test : 0.01 Valeurs critiques : 0.005497 et 0.07828 .

Décision : «H_0^{(3)} est vraie».

P-valeur du test 1a : 0.0512 .
Approximation de la puissance a posteriori du test : 0.1416 .

La procédure interactive donne quant à elle :

Test3Asym1Prop_Int(), réponse :
Saisir le nombre de «un» : 3, réponse :
Saisir la taille de l’échantillon : 210, réponse :
Saisir la première proportion P1 : 0.035, réponse :
Saisir la deuxième proportion P2 : 0.045, réponse :
Saisir le seuil du test : .01, réponse :
les mêmes résultats que ceux de la procédure non interactive sont alors affichés.

Contrairement aux exemples des Alternatives 1a et Alternatives 1b, comme ci-avant, il a fallu augmenter la taille de l'échantillon parce que la première valeur critique était négative. La décision est «\({\cal H}_0^{(3)}\) est vraie». Le test n’est pas significatif. La puissance asymptotique a posteriori est relativement faible : 0,1416. La décision est risquée. Pour être plus sûrs il faudrait augmenter l’échantillonnage. Nous pouvons calculer une approximation de la puissance asymptotique pour les points \(p=0,01429\) et \(p=0.08\) par exemple. Nous exécutons, après les avoir compilées («sourcée» dans R), les procédures de la Remarque 8 ci-dessus.

Puis3Asym1Prop(210,.035,.045,.01,.01429), réponse : 0.1415
Puis3Asym1Prop(210,0.04,0.01,0.08), réponse : 0.5367.

La procédure interactive, par exemple, donne quant à elle :

Puis3Asym1Prop_Int(), réponse :
Saisir la taille de l’échantillon : 210, réponse :
Saisir la première proportion P1 : .035, réponse :
Saisir la deuxième proportion P2 : .045 réponse :
Saisir seuil du test : .01, réponse :
Saisir le point P où calculer une approximation de la puissance asymptotique : 0.08, réponse : 0.5367 .

Nous pouvons également tracer le graphique d’une approximation de la fonction puissance asymptotique du test avec les commandes suivantes :

plot( function(P) Puis3Asym1Prop(210,.035,.045,.01,P),.0,.1, xlab="p",
ylab="pu", ylim= c(0,0.6), main=Fig 2 Approximation de la puissance\n asymptotique du test 3.", col="green4");
x0=c(.035,.045,.045,.08,.08,.01429,.01429); y0=c(0,0,0.01,0,.5367,0,.1415);
x1=c(.035,.045,0,.08,0,0.01429,0); y1=c(.01,.01,.01,.5367,.5367,.1415,.1415);
segments(x0,y0,x1,y1, col="blue");
points( x=c(.035,0.045,.08,.01429), y=c(.01,.01,.5367,.1415), col="red", pch='.', cex=8), réponse :

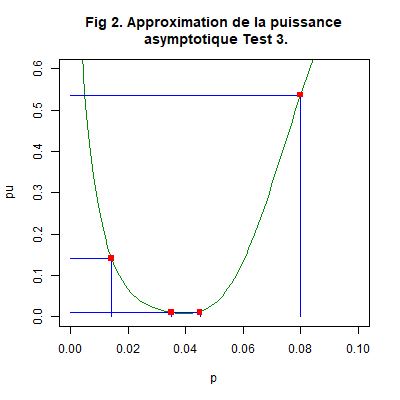
Remarquons que le graphique a l’allure générale de la puissance des tests 3, mais il comporte une asymétrie. Celle-ci est d’autant plus prononcée que l’intervalle n’est pas centré sur \(0,5\). Nous avons marqué en rouge les points de coordonnées \((p_1\ ;\ \alpha)=(0,035\ ;\ 0,01)\), \((p_2\ ;\ \alpha)=(0,045\ ;\ 0,01)\) \((0,01429\ ;\ pu_{\psi^{(3)}_{\infty}}(0,01429))\approx(0,01429\ ;\ 0,1415)\) et \((0,08\ ;\ pu_{\psi^{(3)}_{\infty}}(0,08))\approx(0,08\ ;\ 0,5367)\). Nous constatons, entre autres, que le test est asymptotiquement de seuil \(0,01\) et sans biais. \(\ \square\)

Haut de la page.

7. Tests classiques d’hypothèses.

7. Tests classiques d’hypothèses.

7.5.4.b. Tests asymptotiques sur une proportion théorique - Contre-hypothèses bilatérales.