Contre-hypothèses unilatérales.

7.4.1. Contre-hypothèses unilatérales.

Soit \(X\) une v.a. dont la loi \({\cal L}(X)\) appartient à la famille paramétrique \({\mathfrak L}=\lbrace{\cal L}_{\theta} : \theta\in\Theta\subset{\mathbb R}\rbrace\). La loi \({\cal L}_{\theta}\) est indentifiée par \(l_{\theta}(x)\) qui désigne soit \(P_{\theta}(X=x)\) dans le cas discret, soit la densité \(f(x ; \theta)\) dans le cas continu. Nous avons observé une réalisation \(x_{\bullet}=(x_1, \cdots, x_n)\) d’un \(n\)-échantillon de \(X\). Nous présentons les tests dont les contre-hypothèses sont du type \({\cal H}_1^{(1a)}=\lbrace \theta_0 < \theta\rbrace\) ou bien \({\cal H}_1^{(1b)}=\lbrace \theta_0 > \theta\rbrace\) pour une valeur du paramètre \(\theta=\theta_0\) fixée.

Définition 1. Une famille paramétrique \({\mathfrak L}\) est à rapport de vraisemblance monotone s’il existe une statistique \(T(X_{\bullet})\) telle que pour tous \(\theta, \theta^{\prime} \in \Theta,\ \theta < \theta^{\prime},\) le rapport de vraisemblance s’écrit :

\[ \frac{L(x_{\bullet} ; \theta^{\prime})}{L(x_{\bullet} ; \theta)}=h(T(x_{\bullet})), \]

où \(h(t)\) est une fonction strictement monotone en \(t\). En général la fonction \(h\) dépend des paramètres : \(h(t)=h_{\theta, \theta^{\prime}}(t)\).

Exemple 1. Considérons la loi Gamma \({\cal GA}(\theta ; 1)\) avec \(\Theta={\mathbb R}^{\star}_+\). La densité et la vraisemblance s’écrivent :

\[ f(x ; \theta)=\frac{x^{\theta-1}\exp(-x)}{\Gamma(\theta)}I_{{\mathbb R}_+^{\star}}(x),\quad L(x_{\bullet} ; \theta)=\frac{\displaystyle(\prod_{j=1}^nx_j)^{\theta-1}\exp(-\sum_{j=1}^nx_j)}{\Gamma(\theta)^n}. \]

Pour \(\theta < \theta^{\prime}\) nous avons :

\[ \frac{L(x_{\bullet} ; \theta^{\prime})}{L(x_{\bullet} ; \theta)}=\left(\frac{\Gamma(\theta)}{\Gamma(\theta^{\prime})}\right)^n\exp\left((\theta^{\prime}-\theta)\displaystyle\sum_{j=1}^n\ln(x_j)\right) =h(\sum_{j=1}^n\ln(x_j)). \]

Ainsi, en posant \(h_{\theta, \theta^{\prime}}(t)=\left(\dfrac{\Gamma(\theta)}{\Gamma(\theta^{\prime})}\right)^n\exp\left((\theta^{\prime}-\theta)t\right)\), nous constatons que le rapport de vraisemblance est strictement croissant par rapport à la statistique \(T(X_{\bullet})=\displaystyle\sum_{j=1}^n\ln(X_j).\quad \square\)

Exemple 2. Considérons la loi Exponentielle \({\cal GA}(1 ; \theta)\) avec \(\Theta={\mathbb R}^{\star}_+\). La densité et la vraisemblance s’écrivent :

\[ f(x ; \theta)=\theta\exp(-\theta x)I_{{\mathbb R}_+^{\star}}(x),\quad L(x_{\bullet} ; \theta)=\theta^n\exp(-\theta\sum_{j=1}^nx_j). \]

Pour \(\theta < \theta^{\prime}\) nous avons :

\[ \frac{L(x_{\bullet} ; \theta^{\prime})}{L(x_{\bullet} ; \theta)}=\left(\frac{\theta^{\prime}}{\theta}\right)^n\exp\left(-(\theta^{\prime}-\theta)\displaystyle\sum_{j=1}^nx_j\right) =h(\sum_{j=1}^nx_j). \]

Ainsi, en posant \(h_{\theta, \theta^{\prime}}(t)=\left(\dfrac{\theta^{\prime}}{\theta}\right)^n\exp\left(-(\theta^{\prime}-\theta)t\right)\), nous constatons que le rapport de vraisemblance est strictement décroissant par rapport à la statistique \(T(X_{\bullet})=\displaystyle\sum_{j=1}^n X_j.\quad \square\)

Exemple 3. En fait les deux exemples précédents sont des cas particuliers de la famille exponentielle de lois avec un paramètre unidimensionnel. D’une manière générale pour cette famille, la densité et la vraisemblance s’écrivent :

\[ f(x ; \theta)=\exp\Big( a(\theta)b(x)+c(\theta)+d(x)\Big),\quad L(x_{\bullet} ; \theta)=\exp\left(a(\theta)\sum_{j=1}^nb(x_j)+nc(\theta)+\sum_{j=1}^nd(x_j)\right). \]

Pour \(\theta < \theta^{\prime}\) nous avons :

\[ \frac{L(x_{\bullet} ; \theta^{\prime})}{L(x_{\bullet} ; \theta)}=\exp\left(n(c(\theta^{\prime})-c(\theta))+(a(\theta^{\prime})-a(\theta))\displaystyle\sum_{j=1}^nb(x_j)\right) =h(\sum_{j=1}^nb(x_j)). \]

Ainsi, en posant \(h_{\theta, \theta^{\prime}}(t)=\exp\left(n(c(\theta^{\prime})-c(\theta))+(a(\theta^{\prime})-a(\theta))t\right)\), si la fonction \(a(\theta)\) est strictement monotone, alors le rapport de vraisemblance est monotone par rapport à la statistique \(T(X_{\bullet})=\displaystyle\sum_{j=1}^n b(X_j).\quad \square\)

Propriété 1. Soit \({\mathfrak L}\) une famille paramétrique à rapport de vraisemblance croissant par rapport à la statistique \(T(X_{\bullet})\). Soit \(\theta_0\in\Theta\) et \(\alpha\in \rbrack 0\ ;\ 1\lbrack\) un seuil fixé. Le test \(\psi^{\star}\) défini par :

\[ \psi^{\star}(x_{\bullet})=\gamma_{\alpha}I_{\lbrace T(x_{\bullet})=c_{\alpha}\rbrace}(x_{\bullet})+I_{\lbrace c_{\alpha} < T(x_{\bullet})\rbrace}(x_{\bullet}), \]

où les constantes \(\gamma_{\alpha}\) et \(c_{\alpha}\) sont déterminées par la relation \({\mathbb E}_{\theta_0}\lbrack \psi^{\star}(X_{\bullet})\rbrack=\alpha\), satisfait aux propriétés suivantes :

\({\mathbb E}_{\theta}\lbrack\psi^{\star}(X_{\bullet})\rbrack \geq {\mathbb E}_{\theta}\lbrack\psi(X_{\bullet})\rbrack\), pour tout \(\theta > \theta_0\) et tout \(\psi\) tel que \({\mathbb E}_{\theta_0}\lbrack\psi(X_{\bullet})\rbrack=\alpha\),
\({\mathbb E}_{\theta}\lbrack\psi^{\star}(X_{\bullet})\rbrack \leq {\mathbb E}_{\theta}\lbrack\psi(X_{\bullet})\rbrack\), pour tout \(\theta \leq \theta_0\) et tout \(\psi\) tel que \({\mathbb E}_{\theta_0}\lbrack\psi(X_{\bullet})\rbrack=\alpha\),
\({\mathbb E}_{\theta}\lbrack\psi^{\star}(X_{\bullet})\rbrack\) est une fonction strictement croissante de \(\theta\).

Fixons \(\theta\) tel que \(\theta > \theta_0\). Pour déterminer le maximum de \({\mathbb E}_{\theta}\lbrack\psi(X_{\bullet})\rbrack\) sous la contrainte \({\mathbb E}_{\theta_0}\lbrack\psi(X_{\bullet})\rbrack=\alpha\), il suffit de calculer, pour une constante \(k\), le maximum de \({\mathbb E}_{\theta}\lbrack\psi(X_{\bullet})\rbrack-k{\mathbb E}_{\theta_0}\lbrack\psi(X_{\bullet})\rbrack\) sous la même contrainte. Ce maximum est atteint pour :

\[ \psi^{\star}(x_{\bullet})=\gamma_{\alpha}I_{\lbrace L(x_{\bullet} ; \theta)=k_{\alpha}L(x_{\bullet} ; \theta_0)\rbrace}(x_{\bullet}) + I_{\lbrace L(x_{\bullet} ; \theta)> k_{\alpha}L(x_{\bullet} ; \theta_0)\rbrace}(x_{\bullet}), \]

les constantes \(\gamma_{\alpha}\) et \(k_{\alpha}\) étant déterminées par la relation :

\[ {\mathbb E}_{\theta_0}\lbrack \psi^{\star}(X_{\bullet})\rbrack=\alpha=\gamma_{\alpha}P_{\theta_0}\Big(L(X_{\bullet} ; \theta)=k_{\alpha}L(X_{\bullet} ; \theta_0)\Big) + P_{\theta_0}\Big(L(x_{\bullet} ; \theta)>k_{\alpha}L(x_{\bullet} ; \theta_0)\Big). \]

La condition sur le rapport de vraisemblance implique l’égalité des événements :

\[ \lbrace L(X_{\bullet} ; \theta)=k_{\alpha}L(X_{\bullet} ; \theta_0)\rbrace = \lbrace T(X_{\bullet})=c_{\alpha}\rbrace \quad {\text et}\quad \lbrace L(x_{\bullet} ; \theta)>k_{\alpha}L(x_{\bullet} ; \theta_0))\rbrace = \lbrace c_{\alpha}< T(X_{\bullet})\rbrace. \]

Nous constatons que le test \(\psi^{\star}(x_{\bullet})\) et les constantes \(\gamma_{\alpha}\) et \(c_{\alpha}\) ne dépendent pas de \(\theta\) mais uniquement de \(\theta_0\). C’est le test recherché. La deuxième inégalité s’obtient de manière analogue. La troisième découle de la Propriété 2 du test fondamental, qui est sans biais.\(\quad \square\)

Alternatives 1a.

Soit donnée \({\mathfrak L}\) une famille paramétrique dont le paramètre varie dans \(\Theta\) et \(\theta_0\in\Theta\) fixé. Nous considérons l’alternative :

\({\cal H}_0^{(1a)}=\lbrace\theta\leq\theta_0\rbrace\quad\) contre \(\quad{\cal H}_1^{(1a)}=\lbrace \theta_0 < \theta\rbrace\).

De plus pour \(\theta^{\prime}, \theta^{\prime\prime}\in\Theta,\ \theta^{\prime} < \theta_0 < \theta^{\prime\prime}\) fixés nous considérons également les alternatives suivantes :

\({\cal H}_0^{(1a)}=\lbrace\theta=\theta_0\rbrace\quad\) contre \(\quad{\cal H}_1^{(1a)}=\lbrace \theta_0 < \theta\rbrace\),
\({\cal H}_0^{(1a)}=\lbrace\theta\in\lbrack\theta^{\prime}\ ;\ \theta_0\rbrack \rbrace\quad\) contre \(\quad{\cal H}_1^{(1a)}=\lbrace \theta_0 < \theta\rbrace\),
\({\cal H}_0^{(1a)}=\lbrace\theta\leq \theta_0\rbrace\quad\) contre \(\quad{\cal H}_1^{(1a)}=\lbrace \theta^{\prime\prime} < \theta\rbrace\),
\({\cal H}_0^{(1a)}=\lbrace\theta=\theta_0\rbrace\quad\) contre \(\quad{\cal H}_1^{(1a)}=\lbrace \theta^{\prime\prime} < \theta\rbrace\),
\({\cal H}_0^{(1a)}=\lbrace\theta\in\lbrack\theta^{\prime}\ ;\ \theta_0\rbrack \rbrace\quad\) contre \(\quad{\cal H}_1^{(1a)}=\lbrace \theta^{\prime\prime} < \theta\rbrace\).

Sauf confusions possibles, chacune de ces six alternatives sera toujours désignée Alternative 1a. C’est la première qui le plus utilisée et elle représentera l’ensemble de ces alternatives.

Remarque 1. Si décider à tort que la valeur du paramètre \(\theta\) est supérieure à \(\theta_0\) a les conséquences les plus défavorables pour l’utilisateur, c’est l'Altenative 1a qu’il faut utiliser.

Propriété 2. Nous supposons que la famille paramétrique \({\mathfrak L}\) est à rapport de vraisemblance croissant par rapport à la statistique \(T(X_{\bullet})\). Soit \(\alpha\in \rbrack 0\ ;\ 1\lbrack\) un seuil fixé. Pour tester chacune des six Alternatives 1a ci-dessus, nous considérons le même test :

\[ \psi^{(1a)}(x_{\bullet})=\gamma_{\alpha}I_{\lbrace T(x_{\bullet})=c_{\alpha}\rbrace}(x_{\bullet})+I_{\lbrace c_{\alpha} < T(x_{\bullet})\rbrace}(x_{\bullet}), \]

où les constantes \(\gamma_{\alpha}\) et \(c_{\alpha}\) sont déterminées par la relation :

\[ {\mathbb E}_{\theta_0}\lbrack \psi^{(1a)}(X_{\bullet})\rbrack=\alpha=\gamma_{\alpha}P_{\theta_0}\Big(T(X_{\bullet})=c_{\alpha}\Big) + P_{\theta_0}\Big(T(X_{\bullet}) > c_{\alpha}\Big). \]

Pour chacune des alternatives, ce test est de seuil \(\alpha\), sans biais et U.P.P. à ce seuil; la fonction puissance \({\mathbb E}_{\theta}\lbrack\psi^{(1a)}(X_{\bullet})\rbrack\) n’est définie que pour \(\theta\in{\cal H}_0^{(1a)}\bigcup{\cal H}_1^{(1a)}\) dans chaque alternative. Si de plus \({\mathbb E}_{\theta}\left\lbrack \ln(\dfrac{l_{\theta}(X)}{l_{\theta_0}(X)})\right\rbrack < +\infty, \forall \theta\in{\cal H}_0^{(1a)}\bigcup{\cal H}_1^{(1a)}\), alors il est également convergent. Ainsi la procédure optimale de décision se résume de la maniètre suivante :

Si \(T(x_{\bullet}) < c_{\alpha}\), nous décidons «\({\cal H}_0^{(1a)}\) est vraie».
Si \(T(x_{\bullet}) = c_{\alpha}\), nous décidons «\({\cal H}_1^{(1a)}\) est vraie» avec une probabilité \(\gamma_{\alpha}\) ;
nous réalisons \(u\) de loi \({\cal U}(\rbrack 0\ ;\ 1\lbrack)\) et si \(u < \gamma_{\alpha}\) nous décidons «\({\cal H}_1^{(1a)}\)est vraie», si \(u \geq \gamma_{\alpha}\) nous décidons «\({\cal H}_0^{(1a)}\) est vraie».
Si \(T(x_{\bullet}) > c_{\alpha}\), nous décidons «\({\cal H}_1^{(1a)}\) est vraie».

Cet énoncé est une conséquence directe de la Propriété 1 ci-dessus, ainsi que de la Propriété 2 et de la Propriété 3 du test fondamental.\(\quad \square\)

Remarque 2. Si nous étudions une loi continue alors \(P_{\theta_0}(T(X_{\bullet})=c_{\alpha})=0\). En pratique, nous pouvons, pour ne pas avoir \(T(x_{\bullet})=c_{\alpha}\), calculer \(T(x_{\bullet})\) avec un chiffre décimal de plus que \(c_{\alpha}\) ou inversement. Nous pouvons également fixer \(\gamma_{\alpha}=0\), cela ne change rien aux propriétés du test. Nous décidons alors :

«\({\cal H}_0^{(1a)}\) est vraie» si \(T(x_{\bullet}) \leq c_{\alpha}\),
«\({\cal H}_1^{(1a)}\) est vraie» si \(c_{\alpha} < T(x_{\bullet})\).

Dans le cas discret, en général \(P_{\theta_0}(T(X_{\bullet})=c_{\alpha}) > 0\). Cependant nous pouvons, pour faciliter les calculs, poser \(\gamma_{\alpha}=0\). La décision se prendra de la même manière que ci-dessus, mais alors, comme \(\alpha \leq P_{\theta_0}(c_{\alpha}\leq T(X_{\bullet}))\), le seuil sera inférieur à \(\alpha\) et nous perdrons légèrement de la puissance.

Remarque 3. Si la famille de lois \({\mathfrak L}\) est à rapport de vraisemblance décroissant alors c’est le test \(\psi^{(1b)}\), décrit ci-dessous qu’il faut mettre en œuvre.

Altenatives 1b.

Soit donnée \({\mathfrak L}\) une famille paramétrique dont le paramètre varie dans \(\Theta\) et \(\theta_0\in \Theta\) fixé. Nous considérons l’alternative :

\({\cal H}_0^{(1b)}=\lbrace\theta_0 \leq \theta\rbrace\quad\) contre \(\quad{\cal H}_1^{(1b)}=\lbrace \theta < \theta_0\rbrace\)

De plus pour \(\theta^{\prime}, \theta^{\prime\prime}\in\Theta,\ \theta^{\prime} < \theta_0 < \theta^{\prime\prime}\) fixés nous considérons également les alternatives suivantes :

\({\cal H}_0^{(1b)}=\lbrace\theta=\theta_0\rbrace\quad\) contre \(\quad{\cal H}_1^{(1b)}=\lbrace \theta < \theta_0\rbrace\),
\({\cal H}_0^{(1b)}=\lbrace\theta\in\lbrack\theta_0\ ;\ \theta^{\prime\prime}\rbrack \rbrace\quad\) contre \(\quad{\cal H}_1^{(1b)}=\lbrace \theta < \theta_0\rbrace\),
\({\cal H}_0^{(1b)}=\lbrace\theta_0\leq \theta\rbrace\quad\) contre \(\quad{\cal H}_1^{(1b)}=\lbrace \theta < \theta^{\prime}\rbrace\),
\({\cal H}_0^{(1b)}=\lbrace\theta=\theta_0\rbrace\quad\) contre \(\quad{\cal H}_1^{(1b)}=\lbrace \theta < \theta^{\prime}\rbrace\),
\({\cal H}_0^{(1b)}=\lbrace\theta\in\lbrack\theta_0\ ;\ \theta^{\prime\prime}\rbrack \rbrace\quad\) contre \(\quad{\cal H}_1^{(1b)}=\lbrace \theta < \theta^{\prime}\rbrace\).

Sauf confusions possibles, chacune de ces six alternatives sera toujours appelée Altenative 1b. C’est la première alternative qui les plus utilisée et elle représentera l’ensemble de ces alternatives.

Remarque 4. Si décider à tort que la valeur du paramètre \(\theta\) est inférieure à \(\theta_0\) a les conséquences les plus d favorables pour l’utilisateur, c’est l'Altenative 1b qu’il faut utiliser.

Propriété 3. Nous supposons que la famille paramètrique \({\mathfrak L}\) est à rapport de vraisemblance croissant (resp. décroissant) par rapport à la statistique \(T(X_{\bullet})\). Soit \(\alpha\in \rbrack 0\ ;\ 1\lbrack\) un seuil fixé. Pour tester chacune des six Alternatives 1b ci-dessus nous considérons le même test :

\[ \psi^{(1b)}(x_{\bullet})=\gamma_{\alpha}I_{\lbrace T(x_{\bullet})=c_{\alpha}\rbrace}(x_{\bullet})+I_{\lbrace T(x_{\bullet}) < c_{\alpha}\rbrace}(x_{\bullet}), \] \[ \left({\it resp.}\quad \psi^{(1a)}(x_{\bullet})=\gamma_{\alpha}I_{\lbrace T(x_{\bullet})=c_{\alpha}\rbrace}(x_{\bullet})+I_{\lbrace c_{\alpha} < T(x_{\bullet})\rbrace}(x_{\bullet})\right). \]

où les constantes \(\gamma_{\alpha}\) et \(k_{\alpha}\) sont calculées en utilisant la relation :

\[ \alpha={\mathbb E}_{\theta_0}\lbrack \psi^{(1b)}(X_{\bullet})\rbrack=\gamma_{\alpha}P_{\theta_0}\Big(T(X_{\bullet})=c_{\alpha}\Big) + P_{\theta_0}\Big(T(X_{\bullet}) < c_{\alpha}\Big) \] \[ {\it (resp.}\quad \alpha={\mathbb E}_{\theta_0}\lbrack \psi^{(1a)}(X_{\bullet})\rbrack=\gamma_{\alpha}P_{\theta_0}\Big(T(X_{\bullet})=c_{\alpha}\Big) + P_{\theta_0}\Big(T(X_{\bullet}) > c_{\alpha}\Big)). \]

Pour chacune des alternatives, ce test est de seuil \(\alpha\), sans biais et U.P.P. à ce seuil ; la fonction puissance \({\mathbb E}_{\theta}\lbrack\psi^{(1a)}(X_{\bullet})\rbrack\) n’est définie que pour \(\theta\in{\cal H}_0^{(1b)}\bigcup{\cal H}_1^{(1b)}\) dans chaque alternative. Si de plus \({\mathbb E}_{\theta}\left\lbrack \ln(\dfrac{l_{\theta}(X)}{l_{\theta_0}(X)})\right\rbrack < +\infty, \forall \theta\in{\cal H}_0^{(1b)}\bigcup{\cal H}_1^{(1b)}\), alors il est également convergent. Ainsi la procédure optimale de décision se résume de la manière suivante :

Si \(T(x_{\bullet}) > c_{\alpha}\) (resp. \(T(x_{\bullet}) < c_{\alpha}\)), nous décidons «\({\cal H}_0^{(1b)}\) est vraie».
Si \(T(x_{\bullet}) = c_{\alpha}\), nous décidons «\({\cal H}_1^{(1b)}\) est vraie» avec une probabilité \(\gamma_{\alpha}\) ;
nous réalisons \(u\) de loi \({\cal U}(\rbrack 0\ ;\ 1\lbrack)\) et si \(u < \gamma_{\alpha}\) nous décidons «\({\cal H}_1^{(1b)}\) est vraie», si \(u \geq \gamma_{\alpha}\) nous décidons «\({\cal H}_0^{(1b)}\) est vraie».
Si \(T(x_{\bullet}) < c_{\alpha}\) (resp. \(T(x_{\bullet}) > c_{\alpha}\)) , nous décidons «\({\cal H}_1^{(1b)}\) est vraie».

Pour le voir il suffit d’utiliser la même démarche que celle de la Propriété 2 ci-dessus.\(\quad \square\)

Les indications de la Remarque 2 ci-dessus est encore valable pour tous ces six tests.

Remarque 5. Pour résumer les différents tests et alternatives, pour chaque alternative il faut choisir le test qui permet de décider «\({\cal H}_1^{(1a)}\) est vraie» ou «\({\cal H}_1^{(1b)}\)est vraie» avec \( T(X_{\bullet} > c_{\alpha}\) ou avec \(T(X_{\bullet}) < c_{\alpha}\) dans le même sens (resp. sens contraire) de la contre-hypothèse considérée, selon que le rapport de vraisemblance est croissant (resp. décroissant) par rapport à la statistique \(T(X_{\bullet})\). Nous utilisons le choix du meilleur test avec le tableau suivant :

	Contre-hypothèses	\({\cal H}_1^{(1a)}\)	\({\cal H}_1^{(1b)}\)
Rapport de vraisemblance	Croissant	\(\psi^{(1a)}\)	\(\psi^{(1b)}\)
Rapport de vraisemblance	Décroissant	\(\psi^{(1b)}\)	\(\psi^{(1a)}\)

Exemple 4. Une usine de fabrication de matériel informatique reçoit un lot de composants et procède à un contrôle de réception. Un composant est soit défectueux soit ne l’est pas et ceci indépendamment des autres composants. Le contrôle d’un composant induit la réalisation d’une v.a. \(X\) qui suit une loi de Bernoulli \({\cal B}(1\ ;\ p)\), où \(p\) est la proportion de composants défectueux dans le lot. Le coût de l’arrêt de la fabrication dû à un composant défectueux est tel que, si la proportion \(p\) est supérieure à \(6 \%\), le lot doit être refusé. Nous tirons au hasard \(n=120\) composants et nous constatons 1 seul défectueux ; faut-il accepter le lot ?

Nous supposons que l’acceptation à tort d’un lot a des conséquences plus fâcheuses que le refus à tort de celui-ci. Nous proposons en conséquence de tester l’alternative :

\({\cal H}_0^{(1b)}=\lbrace p\geq 0,06 \rbrace\quad\) contre \(\quad{\cal H}_1^{(1b)}=\lbrace p < 0,06\rbrace\).

Pour \(x_{\bullet}=(x_1,\ \cdots,\ x_n)\) nous avons \(L(x_{\bullet}\ ;\ p)= p^{\sum_{j=1}^nx_j}(1-p)^{n-\sum_{j=1}^nx_j}\). Nous en déduisons, pour \(p_1,\ p_2 \in \rbrack 0\ ;\ 1\lbrack\) :

\[ \frac{L(x_{\bullet}\ ;\ p_2)}{L(x_{\bullet}\ ;\ p_1)}=\left(\frac{p_2(1-p_1)}{p_1(1-p_2)}\right)^{\displaystyle\sum_{j=1}^nx_j}\left(\frac{1-p_2}{1-p_1}\right)^{\displaystyle n}. \]

Ainsi \(p_1 < p_2\) implique que nous sommes en présence d’une famille à rapport de vraisemblance croissant par rapport à la statistique \(\displaystyle T(X_{\bullet})=\sum_{j=1}^nX_j\). De la Propriété 3 ci-dessus nous savons que, pour un nombre donné \(\alpha\in \rbrack 0\ ;\ 1\lbrack\), le test :

\[ \psi^{(1b)}(x_{\bullet})=\gamma_{\alpha}I_{\lbrace T(x_{\bullet})=c_{\alpha}\rbrace}(x_{\bullet})+I_{\lbrace T(x_{\bullet}) < c_{\alpha}\rbrace}(x_{\bullet}), \]

où les constantes \(\gamma_{\alpha}\) et \(c_{\alpha}\) sont déterminées par la relation :

\[ {\mathbb E}_{0,06}\lbrack \psi^{(1b)}(X_{\bullet})\rbrack=\gamma_{\alpha}P_{0,06}(T(X_{\bullet})=c_{\alpha})+P_{0,06}(T(X_{\bullet}) < c_{\alpha})=\alpha. \]

est de seuil \(\alpha\), U.P.P. et sans biais. De plus, comme

\[ {\mathbb E}_p\left\lbrack \ln(\dfrac{l_p(X)}{l_{0,06}(X)})\right\rbrack = p\ln\left(\frac{p}{0,06}\right)+(1-p)\ln\left(\frac{1-p}{1-0,06}\right) < +\infty \]

le test est également convergent. La taille de l’échantillon étant supérieure à \(100\), nous fixons \(\alpha=0,01\). Nous savons que \({\cal L}(X)={\cal B}(1\ ;\ 0,06)\) implique que \(T(X_{\bullet})=\sum_{j=1}^{120}X_j\) suit une loi Binomiale \({\cal B}(120\ ;\ 0,06)\). Les commandes dbinom et pbinom nous permettent de construire le tableau suivant :

\(k\)	\(P_{0,06}(T(X_{\bullet})=k)\)	\(P_{0,06}(T(X_{\bullet})\leq k)\)
\(0\)	\(0,000596132\)	\(0,000596132\)
\(1\)	\(0,004566117\)	\(0,00515730\)
\(2\)	\(0,01734153\)	\(0,02249883\)

Nous en déduisons que \(c_{0,01}=2\) et \(\gamma_{0,01}=\dfrac{0,01-0,00515730}{0,01734153}=0,2789691\approx 0,28\). Le test s’écrit :

\[ \psi^{(1b)}(x_{\bullet})= \begin{cases} 1 & \text{si} & \displaystyle\sum_{j=1}^{120}x_j < 2 ,\\ 0,28 & \text{si} & \displaystyle\sum_{j=1}^{10}x_j = 2 ,\\ 0 & \text{si} & \displaystyle\sum_{j=1}^{10}x_j > 2. \end{cases} \]

Nous avons observé un seul composant défectueux ; nous décidons «\({\cal H}_1^{(1b)}=\lbrace p < 0,06\rbrace\) est vraie», le test est significatif ; ainsi nous acceptons le lot et le risque associé à cette décision est \(\alpha\leq 0,01\). Nous pouvons faire confiance à notre décision. La \(p-\)valeur du test est \(P_{0,06}(T(X_{\bullet}) < 1)=0,000596132\) ; comme elle est inférieure à \(\alpha=0.01\), nous prenons évidemment la même décision.

Le graphique ci-dessous donne la partie essentielle de la fonction puissance du test.

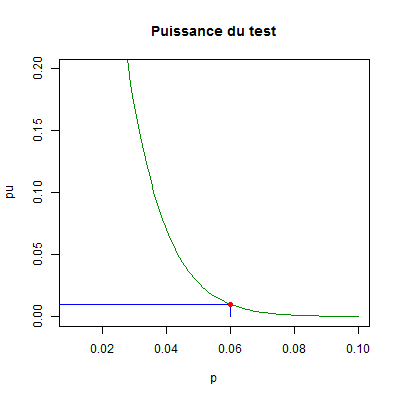
Nous avons marqué en rouge le point de coordonnées \((p_0\ ;\ \alpha)=(0,06\ ;\ 0,01)\). Les propriétés du test sont bien illustrées. \(\quad \square\)

Références. Une étude complète des tests paramétriques se trouve dans les ouvrages de C. Fourgeaud, A. Fuchs (1967) et de E. L. Lehmann, J. P. Romano (2005).

Haut de la page.

7. Tests classiques d’hypothèses.

7. Tests classiques d’hypothèses.

7.4.1. Contre-hypothèses unilatérales.