Contre-hypothèses bilatérales.

7.4.2. Contre-hypothèses bilatérales.

Soit \({\mathfrak L}=\lbrace{\cal L}_{\theta} : \theta\in\Theta\subset{\mathbb R}\rbrace\) une famille paramétrique de lois. Soit \(\theta_0\in \Theta\). Nous considérons l’alternative :

\({\cal H}_0=\lbrace \theta=\theta_0\rbrace \quad\) contre \(\quad{\cal H}_1=\lbrace \theta\not=\theta_0\rbrace\).

Nous avons un résultat négatif.

Propriété 1. Pour tout seuil fixé \(\alpha\in\rbrack 0\ ;\ 1\lbrack\), il n’existe pas de test U.P.P. pour cette alternative.

En effet, si un tel test existait, il serait, en particulier pour une famille à rapport de vraisemblance monotone, U.P.P. pour les deux alternatives :

\({\cal H}_0^{(1a)}=\lbrace \theta=\theta_0\rbrace\quad\) contre \(\quad{\cal H}_1^{(1a)}=\lbrace \theta_0 < \theta\rbrace\) et
\({\cal H}_0^{(1b)}=\lbrace \theta=\theta_0\rbrace\quad\) contre \(\quad{\cal H}_1^{(1b)}=\lbrace \theta < \theta_0\rbrace\).

Ceci contredirait les Propriété 2 et Propriété 3 des tests avec contre-hypothèses unilatérales qui donnent, pour chacune des alternatives ci-dessus, un test U.P.P. différent, pour tout seuil \(\alpha\).\(\quad \square\)

Cependant si nous nous restreignons aux tests sans biais, nous pouvons construire un test U.P.P..

Alternatives 2.

Soit \(\theta_0\in \Theta\). Nous considérons l’alternative :

\({\cal H}_0^{(2)}=\lbrace \theta=\theta_0\rbrace \quad\) contre \(\quad{\cal H}_1^{(2)}=\lbrace \theta\not=\theta_0\rbrace\).

De plus pour \(\theta^{\prime},\ \theta^{\prime\prime}\in\Theta\) avec \(\theta^{\prime} < \theta_0 < \theta^{\prime\prime}\) fixés, nous considérons également les alternatives dont l’hypothèse nulle est \({\cal H}_0^{(2)}\) ci-dessus, et la contre-hypothèse est l’une des hypothèses, encore notée \({\cal H}_1^{(2)}\),

\({\cal H}_1^{(2)}=\lbrace \theta\not\in\lbrack \theta_0\ ;\ \theta^{\prime\prime}\rbrack\rbrace\quad\), \(\quad{\cal H}_1^{(2)}=\lbrace \theta\not\in\lbrack \theta^{\prime}\ ;\ \theta_0\rbrack\rbrace\quad\) ou \(\quad{\cal H}_1^{(2)}=\lbrace \theta\not\in\lbrack \theta^{\prime}\ ;\ \theta^{\prime\prime}\rbrack\rbrace.\)

Sauf confusions possibles, chacune de ces quatre alternatives sera toujours appelée Alternative 2. C’est la première alternative, la plus utilisée, qui représentera cet ensemble d’alternatives.

Remarque 1. Si pour l’utilisateur décider à tort que le paramètre n’est pas égal à une valeur fixée a les conséquences les plus défavorables, c’est sur cette Alternative 2 qu’il doit fonder sa démarche.

Propriété 2. Soit \({\mathfrak L}\) une famille exponentielle à un paramètre unidimensionnel \(\theta\in\Theta \subset{\mathbb R}\) à rapport de vraisemblance monotone par rapport à la statistique \(T(X_{\bullet})\). Soit \(\theta_0\in\Theta\) et un seuil \(\alpha\in \rbrack 0\ ;\ 1\lbrack\) fixés. Pour tester chacune des quatre Alternatives 2 nous utilisons le test :

\[ \psi^{(2)}(x_{\bullet})=\gamma_1I_{\lbrace T(x_{\bullet})=c_1\rbrace}(x_{\bullet})+I_{\lbrace T(X_{\bullet})\not\in \lbrack c_1\ ;\ c_2\rbrack\rbrace}(x_{\bullet})+\gamma_2I_{\lbrace T(x_{\bullet})=c_2\rbrace}(x_{\bullet}). \]

Les constantes \(\gamma_1, \gamma_2, c_1\) et \(c_2\) étant déterminées par les relations :

\[ {\mathbb E}_{\theta_0}\lbrack \psi^{(2)}(X_{\bullet})\rbrack=\gamma_1P_{\theta_0}\Big(T(X_{\bullet})=c_1\Big) + P_{\theta_0}\Big(T(X_{\bullet})\not\in \lbrack c_1\ ;\ c_2\rbrack\Big) + \gamma_2P_{\theta_0}\Big(T(X_{\bullet})=c_2\Big)=\alpha, \]

\[ {\mathbb E}_{\theta_0}\lbrack T(X_{\bullet})\psi^{(2)}(X_{\bullet})\rbrack=\alpha{\mathbb E}_{\theta_0}\lbrack T(X_{\bullet})\rbrack \]

Ce test est de seuil \(\alpha\), sans biais, U.P.P. parmi tous les tests sans biais à ce seuil et convergent. La fonction puissance \({\mathbb E}_{\theta}\lbrack\psi^{(2)}(X_{\bullet})\rbrack\) n’est définie que pour \(\theta\in{\cal H}_0^{(2)}\bigcup{\cal H}_1^{(2)}\) dans chaque alternative. La procédure de décision est la même pour toutes les alternatives 2 :

Si \(c_1 < T(x_{\bullet}) < c_2\), nous décidons «\({\cal H}_0^{(2)}\) est vraie».
Si \(T(x_{\bullet}) = c_i\), nous décidons «\({\cal H}_1^{(2)}\) est vraie» avec une probabilité \(\gamma_i\) ;
nous réalisons \(u\) de loi \({\cal U}(\rbrack 0\ ;\ 1\lbrack)\) et si \(u < \gamma_i\) nous décidons «\({\cal H}_1^{(2)}\) est vraie», si \(u \geq \gamma_i\) nous décidons «\({\cal H}_0^{(2)}\) est vraie» ; ceci pour \(i=1,\ 2\).
Si \(T(x_{\bullet}) < c_1\) ou si \(T(x_{\bullet}) > c_2\), nous décidons «\({\cal H}_1^{(2)}\) est vraie».

Pour le voir nous considérons le test \(\psi^{(3)}\) ci-dessous en faisant tendre \(\theta_1\) (resp. \(\theta_2\)) à gauche (resp. droite) vers \(\theta_0\). Le test \(\psi^{(2)}\) a ainsi les mêmes propriétés que celles de \(\psi^{(3)}\), en particulier nous obtenons la première relation. La deuxième relation permettant de calculer les constantes s’obtient en constatant que \(\psi^{(2)}\) est sans biais et ainsi la fonction \({\mathbb E}_{\theta}\lbrack \psi^{(2)}(X_{\bullet})\rbrack\) atteint son minimum au point \(\theta=\theta_0\). De plus la statistique \(T(X_{\bullet})\) étant exhaustive, nous connaissons la forme de sa densité pour les lois exponentielles. D’où en dérivant sous le signe «somme» nous avons la deuxième relation. \(\quad \square\)

Remarque 2. Il n’existe pas de test pour l’alternative \({\cal H}_0=\lbrace \theta\not=\theta_0\rbrace\) contre \({\cal H}_1=\lbrace \theta=\theta_0\rbrace\).

Remarque 3. Si nous étudions une loi continue alors \(P_{\theta_0}(T(X_{\bullet})=c_i)=0\), pour \(i=1,\ 2\). En pratique, nous pouvons, pour ne pas avoir \(T(x_{\bullet})=c_i,\ i=1,\ 2\), calculer \(T(x_{\bullet})\) avec un chiffre décimal de plus que \(c_i,\ i=1,\ 2\) ou inversement. Nous pouvons également fixer \(\gamma_i=0,\ i=1,\ 2\), cela ne change rien aux propriétés du test. Nous décidons alors :

«\({\cal H}_0^{(2)}\) est vraie» si \(T(x_{\bullet}) \leq c_1\) ou si \(T(x_{\bullet}) \geq c_2\),
«\({\cal H}_1^{(2)}\) est vraie» si \(c_1 < T(x_{\bullet}) < c_2\).

Dans le cas discret, en général \(P_{\theta_0}(T(X_{\bullet})=c_i) > 0\), pour \(i=1,\ 2\). Cependant nous pouvons, pour faciliter les calculs, poser \(\gamma_i=0\), \(i=1,\ 2\). La décision se prendra de la même manière que ci-dessus, mais le seuil sera inférieur à \(\alpha\) et nous perdrons légèrement de la puissance..

Exemple 1. Nous supposons que l’intervalle de temps entre la mise en service et la première panne d’un équipement est une v.a. \(X\) distribuée selon une loi Gamma \({\cal GA}(a\ ;\ b)\). Nous désignons les paramètres avec des lettres latines pour éviter toute confusion avec les seuils. Nous supposons que \(a=a_0=2\) est connu et influence très peu la qualité de fonctionnement de cet équipement, ce qui n’est pas le cas pour le paramètre \(b\). Nous nous proposons de mettre en place le test de l’alternative :

\({\cal H}_0^{(2)}=\lbrace b=1\rbrace\quad\) contre \(\quad{\cal H}_1^{(2)}=\lbrace b\not=1\rbrace\).

Nous réalisons un \(25\)-échantillon de \(X\) et l’enregistrons dans R :

xpoint25 ; réponse :
[1] 1.456 1.486 1.110 1.910 0.444 2.635 0.976 0.780 2.381 0.497 0.135 3.688
[13] 3.712 1.174 1.560 0.600 0.182 0.736 2.570 1.264 0.891 6.809 0.484 0.569
[25] 0.938.

Remarquons que :

\[ L(x_{\bullet}\ ;\ b)=\prod_{j=1}^n\frac{b^{a_0}x_j^{a_0-1}\exp(-bx_j)}{\Gamma(a_0)}=\exp\Big(-b\sum_{j=1}^nx_j+(a_0-1)\sum_{j=1}^n\ln(x_j) -n\ln(\Gamma(a_0))+na_0\ln(b)\Big). \]

Nous sommes en présence d’une famille exponentielle à rapport de vraisemblance monotone par rapport à la statistique \(T(X_{\bullet})=\sum_{j=1}^nX_j\). La Propriété 2 ci-dessus nous fournit, pour un seuil donné \(\alpha\), le test U.P.P., parmi tous les tests sans biais, et convergent. La loi étant continue nous posons \(\gamma_1=\gamma_2=0\). Les deux autres constantes \(c_1\) et \(c_2\) sont déterminées par les relations \({\mathbb E}_{(na_0\ ;\ 1)}\lbrack \psi^{(2)}(X_{\bullet})\rbrack=\alpha\) et \({\mathbb E}_{(na_0\ ;\ 1)}\lbrack \psi^{(2)}(X_{\bullet}T(X_{\bullet}))\rbrack=\alpha{\mathbb E}_{(na_0\ ;\ 1)}\lbrack T(X_{\bullet})\rbrack\). Un calcul simple nous montre que la deuxième condition s’écrit \({\mathbb E}_{(na_0+1\ ;\ 1)}\lbrack \psi^{(2)}(X_{\bullet})\rbrack=\alpha\). Pour calculer ces constantes nous avons construit la procédure GammaTestBilateralBeta0. Après l’avoir compilée («sourcée») dans R, nous l’exécutons avec \(a_0=2,\ b_0=1,\ n=25\) et \(\alpha=0,05\) :

GammaTestBilateralBeta0(2,1,25,0.05) ; réponse : L'intervalle d'acceptation est [ 37.38769 ; 65.22339 ]

Nous avons donc le test :

Si \(37,38769 \leq T(x_{\bullet}) \leq 65,22339\), nous décidons «\({\cal H}_0^{(2)}\) est vraie».
Si \(T(x_{\bullet}) < 37,38769\) ou si \(T(x_{\bullet}) > 65,22339\), nous décidons «\({\cal H}_1^{(2)}\) est vraie».

Nous calculons : sum(xpoint25) ; réponse : 38.987.

C’est-à-dire \(T(x_{\bullet})=\sum_{j=1}^{25}x_j=38,987\). Nous décidons donc «\({\cal H}_0^{(2)}=\lbrace b=1\rbrace\) est vraie». Nous savons par ailleurs que, lorsque \(a_0\) est connu, le meilleur estimateur de \(b\) est \(\dfrac{a_0}{{\overline X}}\) ; nous avons la réalisation \({\widehat b}=\dfrac{2}{{\overline x}}=1,282479\). Nous calculons la puissance en ce point :

\[ pu_{\psi^{(2)}}(1,282479)={\mathbb E}_{1,282479}\lbrack\psi^{(2)}\rbrack=P_{1,282479}(T(X_{\bullet}) < 37,38769)+P_{1.282479}(T(X_{\bullet}) > 65,22339). \]

Nous avons construit la procédure GammaPuissBilateralBeta0 permettant de calculer la puissance du test. Après l’avoir compilée («sourcée») dans R, nous l’exécutons

GammaPuissBilateralBeta0(1.282479,2,1,25,0.05) ; réponse : 0.4025584

Ainsi la puissance a posteriori est de \(0,4025584\) ; elle est trop faible, nous ne pouvons pas avoir confiance en cette décision. Nous réalisons un nouvel échantillon de taille \(40\) et l’enregistrons dans R :

xpoint40 ; réponse :
[1] 2.602 1.427 2.837 2.105 0.957 0.520 0.752 0.847 0.817 1.900 1.926 2.048
[13] 1.885 0.161 1.195 0.661 0.125 1.317 1.634 1.635 0.478 0.947 1.782 0.687
[25] 1.830 1.137 1.256 1.835 2.268 0.636 0.879 0.112 0.581 1.041 1.507 1.095
[37] 2.638 3.028 1.569 2.725

Nous avons alors \(T(X_{\bullet})=\sum_{j=1}^{40}X_j=55,382\) (sum(xpoint40) ; réponse : 55.382). Les valeurs critiques sont à présent :

GammaTestBilateralBeta0(2,1,40,0.05) : réponse : L'intervalle d'acceptation est [ 63.73317 ; 98.89034 ]

Nous décidons donc «\({\cal H}_1^{(2)}=\lbrace b\not=1\rbrace\) est vraie» ; le test est significatif, nous pouvons avoir confiance en notre décision. Nous avons, avec ce nouvel échantillon, \({\widehat b}=\dfrac{2}{\overline x}=1,444513\) et :

GammaPuissBilateralBeta0(1.444513,2,1,40,0.05) ; réponse : 0.9071102

Le graphique suivant des puissaces des tests avec chaque échantillon illustre l’ensemble des résultats numériques que nous avons obtenus. Nous avons marqué en rouge les points de coordonnées \((b_0\ ;\ \alpha)=(1\ ;\ 0,05),\ (1,282479\ ;\ 0,4025584)\) et \((1.444513\ ;\ 0,9071102)\).

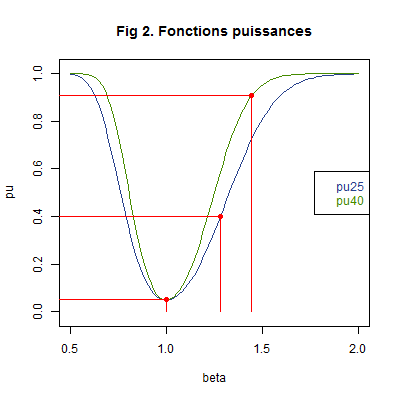
Nous constatons, en particulier, que les risques sont plus faibles pour l’échantillon avec la taille la plus grande. \(\quad \square\)

Le résultat suivant nous permet de calculer facilement, dans certains cas, les contantes du test \(\psi^{(2)}\) :

Propriété 3. Supposons que la loi \({\cal L}_{\theta_0}(T)\) soit symétrique par rapport à un nombre \(t_0\) et qu’un test \(\psi\) soit également symétrique par rapport au même nombre. Alors si nous avons la première relation de la Propriété 2, nous avons la seconde et \(c_2=2t_0-c_1,\ \gamma_1=\gamma_2\).

Pour le voir il suffit de constater que la symétrie \({\cal L}_{\theta_0}(T)\) implique \({\mathbb E}_{\theta_0}\lbrack T(X_{\bullet})\rbrack=t_0\) et d’utiliser celle de \(\psi\). \(\quad \square\)

Alternatives 3.

Soit \({\mathfrak L}=\lbrace{\cal L}_{\theta} : \theta\in\Theta\subset{\mathbb R}\rbrace\) une famille paramétrique de lois. Soit \(\theta_1,\ \theta_2\in \Theta,\ \theta_1 < \theta_2\). Nous considérons l’alternative :

\({\cal H}_0^{(3)}=\lbrace \theta\in \lbrack \theta_1\ ;\ \theta_2\rbrack\rbrace\quad\) contre \(\quad{\cal H}_1^{(3)}=\lbrace \theta\not\in\lbrack \theta_1\ ;\ \theta_2\rbrack\rbrace\).

De plus pour \(\theta^{\prime},\ \theta^{\prime\prime}\in\Theta\) avec \(\theta^{\prime} < \theta_1 < \theta_2 < \theta^{\prime\prime}\) fixés, nous considérons #x00e9;galement les alternatives dont l’hypothèse nulle est soit \({\cal H}_0^{(3)}=\lbrace \theta \in \lbrack \theta_1\ ;\ \theta_2\rbrack\rbrace\) ci-dessus, soit l’hypothèse \({\cal H}_0^{(3)}=\lbrace\theta=\theta_1, \theta_2\rbrace\), et la contre-hypothèse est soit \({\cal H}_1^{(3)}=\lbrace \theta\not\in\lbrack \theta_1\ ;\ \theta_2\rbrack\rbrace\) ci-dessus, soit l’une des hypothèses, encore notée \({\cal H}_1^{(3)}\),

\({\cal H}_1^{(3)}=\lbrace \theta\not\in\lbrack \theta_1\ ;\ \theta^{\prime\prime}\rbrack\rbrace\quad\), \(\quad{\cal H}_1^{(3)}=\lbrace \theta\not\in\lbrack \theta^{\prime}\ ;\ \theta_2\rbrack\rbrace\quad\) ou \(\quad{\cal H}_1^{(3)}=\lbrace \theta\not\in\lbrack \theta^{\prime}\ ;\ \theta^{\prime\prime}\rbrack\rbrace.\)

Sauf confusions possibles, chacune de ces huit alternatives sera toujours notée Alternative 3. C’est la première alternative qui représentera cet ensemble d’alternatives.

Remarque 4. Si pour l’utilisateur décider à tort que le paramètre n’est pas dans un intervalle fixé a les conséquences les plus graves, c’est sur ce test \(\psi^{(3)}(X_{\bullet})\) qu’il doit fonder sa démarche.

Propriété 4. Pour tout seuil \(\alpha\in\rbrack 0\ ;\ 1\lbrack\), il n’existe pas de test U.P.P. pour cette Alternative 3.

La preuve se fait de manière tout à fait analogue à celle de la Propriété 1 ci-dessus. \(\quad \square\)

Propriété 5. Soit \({\mathfrak L}\) une famille exponentielle à un paramètre unidimensionnel \(\theta\in\Theta \subset{\mathbb R}\) à rapport de vraisemblance monotone par rapport à la statistique \(T(X_{\bullet})\). Soit \(\alpha\in \rbrack 0\ ;\ 1\lbrack\) un seuil fixé. Pour tester chacune des huit Alternatives 3 nous utilisons le test :

\[ \psi^{(3)}(x_{\bullet})=\gamma_1I_{\lbrace T(x_{\bullet})=c_1\rbrace}(x_{\bullet})+I_{\lbrace T(X_{\bullet})\not\in \lbrack c_1\ ;\ c_2\rbrack\rbrace}(x_{\bullet})+ \gamma_2I_{\lbrace T(x_{\bullet})=c_2\rbrace}(x_{\bullet}), \]

les constantes \(\gamma_1, \gamma_2, c_1\) et \(c_2\) étant déterminées par les relations

\[ {\mathbb E}_{\theta_i}\lbrack \psi^{(3)}(X_{\bullet})\rbrack=\gamma_1P_{\theta_i}\Big(T(X_{\bullet})=c_1\Big) + P_{\theta_i}\Big(T(X_{\bullet})\not\in \lbrack c_1\ ;\ c_2\rbrack\Big)+ \gamma_2P_{\theta_i}\Big(T(X_{\bullet})=c_2\Big)=\alpha,\ i=1,\ 2. \]

Pour chacune des alternatives précédentes, ce test est de seuil \(\alpha\), sans biais, U.P.P. parmi tous les tests sans biais à ce seuil et convergent. La fonction puissance \(pu_{\psi^{(3)}}(\theta)={\mathbb E}_{\theta}\lbrack \psi^{(3)}(X_{\bullet})\rbrack\) est chaque fois définie pour les valeurs \(\theta \in {\cal H}_0^{(3)}\bigcup{\cal H}_1^{(3)}\). Ainsi la procédure optimale de décision se résume de la maniètre suivante :

Si \(c_1 < T(x_{\bullet}) < c_2\), nous décidons «\({\cal H}_0^{(3)}\) est vraie».
Si \(T(x_{\bullet}) = c_i\), nous décidons «\({\cal H}_1^{(3)}\) est vraie» avec une probabilité \(\gamma_i\) ;
nous réalisons \(u\) de loi \({\cal U}(\rbrack 0\ ;\ 1\lbrack)\) et si \(u < \gamma_i\) nous décidons «\({\cal H}_1^{(3)}\) est vraie», si \(u \geq \gamma_i\) nous décidons «\({\cal H}_0^{(3)}\) est vraie», ceci pour \(i=1,\ 2\).
Si \(T(x_{\bullet}) < c_1\) ou si \(T(x_{\bullet}) > c_2\), nous décidons «\({\cal H}_1^{(3)}\) est vraie».

En effet, soit \(\psi^{(4)}\) le test optimal construit à la Propriété 2 pour l’Alternative 4, \({\cal H}_0^{(4)}=\lbrace \theta \not\in \rbrack \theta_1\ ;\ \theta_2\lbrack\rbrace\) contre \({\cal H}_1^{(4)}=\lbrace \theta\in\rbrack \theta_1\ ;\ \theta_2\lbrack\rbrace\), avec un seuil \(\widehat{\alpha}=1-\alpha\) et posons \(\psi^{(3)}=1-\psi^{(4)}\). Les constantes sont égales à \(c_i=\widehat{c}_i\) et \(\gamma_i=1-\widehat{\gamma}_i\), pour \(i=1, 2\). Il est alors relativement aisé de prouver que ce dernier test est celui de l’énoncé et satisfait aux propriétés de celui-ci.\(\quad \square\)

Remarque 5. Si nous étudions une loi continue alors \(P_{\theta_i}(T(X_{\bullet})=c_{i^{\prime}})=0\), pour \(i,\ i^{\prime}=1,\ 2\). En pratique, pour ne pas avoir \(T(x_{\bullet})=c_i,\ i=1,\ 2\), nous pouvons calculer \(T(x_{\bullet})\) avec un chiffre décimal de plus que \(c_i,\ i=1,\ 2\) ou inversement. Nous pouvons également fixer \(\gamma_i=0,\ i=1,\ 2\), cela ne change rien aux propriétés du test. Nous décidons alors :

«\({\cal H}_0^{(3)}\) est vraie» si \(c_1 \leq T(x_{\bullet}) \leq c_2\),
«\({\cal H}_1^{(3)}\) est vraie» si \(T(x_{\bullet}) \not\in \lbrack c_1\ ;\ c_2\rbrack\).

Dans le cas discret, en général \(P_{\theta_i}(T(X_{\bullet})=c_{i^{\prime}}) > 0\), pour \(i,\ i^{\prime}=1,\ 2\). Cependant nous pouvons, pour faciliter les calculs, poser \(\gamma_i=0\), \(i=1,\ 2\). La décision se prendra de la même manière que ci-dessus, mais le seuil sera inférieur à \(\alpha\) et nous perdrons légèrement de la puissance.

Exemple 2. Nous supposons que le nombre de personnes par unité de temps dans une file d’attente est une v.a. \(X\) distribuée selon une loi de Poisson \({\cal P}(\lambda)\). Cette file d’attente dessert un nombre fixe de guichets. Ce nombre et le temps d’attente sont «raisonnables» lorsque \(5\leq \lambda\leq 8\). Nous nous proposons de tester l’alternative :

\({\cal H}_0^{(3)}=\lbrace \lambda\in \lbrack 5\ ;\ 8\rbrack\rbrace\quad\) contre \(\quad{\cal H}_1^{(3)}=\lbrace \lambda\not\in\lbrack 5\ ;\ 8\rbrack\rbrace\).

Nous réalisons un \(20\)-échantillon de \(X\) et l’enregistrons dans R :

xpoint20 ; réponse : 4 3 6 4 4 2 5 7 7 6 5 4 4 2 5 3 3 3 5 5.

Remarquons que :

\[ L(x_{\bullet}\ ;\ \lambda)=\prod_{j=1}^n\frac{\lambda^{x_j}\exp(-\lambda)}{x_j!}=\exp\Big(\ln(\lambda)\sum_{j=1}^nx_j-\lambda+\sum_{j=1}^n\ln(x_j!)\Big). \]

Nous sommes en présence d’une famille exponentielle à rapport de vraisemblance monotone par rapport à la statistique \(T(X_{\bullet})=\sum_{j=1}^nX_j\). La Propriété 5 ci-dessus nous fournit, pour un seuil donné, le test U.P.P., parmi tous les tests sans biais, et convergent. Les quatre constantes \(c_1,\ \gamma_1,\ c_2\) et \(\gamma_2\) sont déterminées par les relations \({\mathbb E}_{\lambda_1}\lbrack \psi^{(3)}(X_{\bullet})\rbrack=\alpha={\mathbb E}_{\lambda_2}\lbrack \psi^{(3)}(X_{\bullet})\rbrack\). Pour ce faire nous avons construit la procédure PoissonTestBilateral12. Après l’avoir compilée(«sourcée») dans R, nous l’exécutons avec \(n=20\) et \(\alpha=0,05\) :

PoissonTestBilateral12(5,8,20,0.05) ; réponse :
La valeur critique c1 est 84 avec gamma1 0.3277988
La valeur critique c2 est 181 avec gamma2 0.4028122
Une réalisation de U(]0 ; 1[) est 0.294693

Nous avons donc le test :

Si \(84 < T(x_{\bullet}) < 181\), nous décidons «\({\cal H}_0^{(3)}\) est vraie».
Si \(T(x_{\bullet}) = 84\) (resp. \(181\)), nous décidons «\({\cal H}_1^{(3)}\) est vraie» avec une probabilité \(0,3277988\) (resp. \(0,4028122\)) ;
nous réalisons \(u\) de loi \({\cal U}(\rbrack 0\ ;\ 1\lbrack)\) et si \(u < 0,3277988\) (resp. \(0,4028122\)) nous décidons «\({\cal H}_1^{(3)}\) est vraie», si \(u \geq 0,3277988\) (resp. \(0,4028122\)) nous décidons «\({\cal H}_0^{(3)}\) est vraie».
Si \(T(x_{\bullet}) < 84\) ou si \(T(x_{\bullet}) > 181\), nous décidons «\({\cal H}_1^{(3)}\) est vraie».

Nous calculons :

sum(xpoint20) ; réponse : 87.

C’est-à-dire \(T(x_{\bullet})=\sum_{j=1}^{20}x_j=87\). Nous décidons donc «\({\cal H}_0^{(3)}=\lbrace \lambda\in \lbrack 5\ ;\ 8\rbrack\rbrace\) est vraie». Remarquons que si nous avions observé \(T(x_{\bullet})=\sum_{j=1}^{20}x_j=84\), la procédure nous ayant fourni une simulation de la loi \({\cal U}(\rbrack 0\ ;\ 1\lbrack)\), \(u=0.294693\), et celle-ci étant inférieure à \(\gamma_1=0,3277988\), nous aurions dû décider «\({\cal H}_1^{(3)}=\lbrace \lambda\not\in \lbrack 5\ ;\ 8\rbrack\rbrace\) est vraie». Comme \({\cal H}_0^{(3)}\) est un intervalle nous n’avons pas de \(p-\)valeur. Nous savons par ailleurs que \({\overline X}\) est le meilleur estimateur de \(\lambda\) ; nous avons la réalisation \({\widehat \lambda}={\overline x}=4,35\) (mean(xpoint20) ; réponse : 4.35), qui se trouve dans \({\cal H}_1^{(3)}=\lbrace \lambda\not\in\lbrack 5\ ;\ 8\rbrack\rbrace\); nous calculons la puissance en ce point :

\[ pu_{20}(4,35)={\mathbb E}_{4,35}\lbrack\psi^{(3)}\rbrack= \] \[ =P_{4,35}(T(X_{\bullet}) < 84)+0,3277988*P_{4,35}(T(X_{\bullet}) = 84)+0,4028122*P_{4,35}(T(X_{\bullet}) = 181)+P_{4,35}(T(X_{\bullet}) > 181). \]

Nous avons construit la procédure PoissonPuissBilateral12 permettant de calculer la puissance du test. Après l’avoir compilée («sourcée») dans R, nous l’exécutons

PoissonPuissBilateral12(4.35,5,8,20,.05) ; réponse : 0.373033

Ainsi la puissance a posteriori est de \(0,373033\) ; elle est trop faible, nous ne pouvons pas faire confiance à cette décision. Nous réalisons un nouvel échantillon de taille \(60\) et l’enregistrons dans R :

xpoint60 ; réponse :
3 8 6 6 8 4 6 5 1 5 1 4 6 0 4 4 10 1 3 2 5 3 3 3 6
[26] 6 3 5 4 2 5 7 3 3 2 1 6 8 7 4 1 9 3 3 5 3 9 5 1 2
[51] 4 0 5 8 2 5 5 2 4 9

Nous avons à présent \(T(x_{\bullet})=\sum_{j=1}^{60}x_j=258\) (sum(xpoint60) ; réponse : 258). Les valeurs critiques sont :

PoissonTestBilateral12(5,8,60,.05) : réponse :
La valeur critique c1 est 272 avec gamma1 0.290793
La valeur critique c2 est 516 avec gamma2 0.178182
Une réalisation de U(]0 ; 1[) est 0.0104239

Nous décidons donc «\({\cal H}_1^{(3)}=\lbrace \lambda\not\in \lbrack 5\ ;\ 8\rbrack\rbrace\) est vraie». Comme le test est significatif, nous faisons confiance à notre décision. Remarquons que pour cet échantillon nous avons : \({\widehat \lambda}={\overline x}=4,3\) (mean(xpoint60) ; réponse : 4.3).

Le graphique suivant des puissances des tests avec chaque échantillon illustre l’ensemble des résultats numériques que nous avons obtenus. Nous avons marqué en rouge les points de coordonnées \((\lambda_1\ ;\ \alpha)=(5\ ;\ 0,05),\ (\lambda_2\ ;\ \alpha)=(8\ ;\ 0,05),\ (4,3\ ;\ 0,805393)\) et \((4,35\ ;\ 0,373033)\).

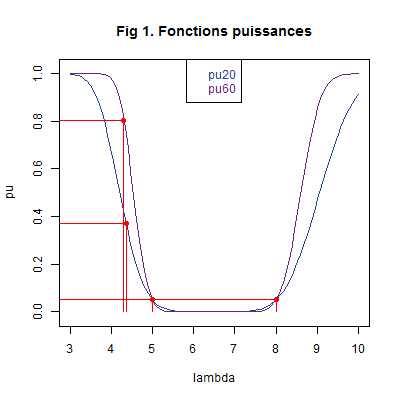
Nous constatons, en particulier, que les risques sont plus faibles pour l’échantillon avec la taille la plus grande. \(\quad \square\)

Références. Une étude complète des tests paramétriques se trouve dans les ouvrages de C. Fourgeaud, A. Fuchs (1967) et de E. L. Lehmann, J. P. Romano (2005).

Haut de la page.

7. Tests classiques d’hypothèses.

7. Tests classiques d’hypothèses.

7.4.2. Contre-hypothèses bilatérales.