

Soit \(X\) une v.a. et \(X_{\bullet}\) un \(n\)-échantillon de celle-ci. Nous considérons deux ensembles disjoints de lois \({\mathfrak L}_0\), \({\mathfrak L}_1\) et \(\psi\) un test de l’alternative :
Définition 1. Nous appelons risque de première espèce du test \(\psi\) associé à la loi \({\cal L}\in{{\mathfrak L}_0}\) le nombre :
\[ \alpha_{\psi}({\cal L})={\mathbb E}_{\cal L}\lbrack \psi(X_{\bullet})\rbrack=P_{\cal L}(\psi(X_{\bullet})=1). \]Nous appelons seuil de signification du test \(\psi\) le plus petit nombre \(\alpha\in\rbrack 0\ ;\ 1\lbrack\) tel que : \(\alpha_{\psi}({\cal L})\leq\alpha, \quad\forall {\cal L}\in{{\mathfrak L}_0}\).
Interprétation. Le risque de première espèce correspond à la probabilité de l’erreur de première espèce, c’est-à-dire celle de décider «\({\cal H}_1\) est vraie» à tort lorsque \({\cal H}_0\) est vraie. C’est, selon notre principe général, la probabilité sous \({\cal H}_0\) de l’événement rare, dont la réalisation impliquera la décision «\({\cal H}_1\) est vraie», ou, ce qui est pareil, «le test est significatif». Le seuil de signification est une barrière que le risque de première espèce ne peut pas franchir.
Remarque 1. Le seuil de signification est aussi appelé risque \(\alpha\) ou encore simplement seuil. Les nombres \(\alpha_{\psi}({\cal L})\) pour \({\cal L}\in{{\mathfrak L}_0}\) et \(\alpha\) sont très souvent exprimés en pourcentage. C’est l’utilisateur qui fixe le seuil ; d’habitude \(\alpha=0,05\) ou \(5 \%\). En général, et plus particulièrement pour les lois continues dans les cas paramétriques, il existe au moins une loi de \({\mathfrak L}_0\) pour laquelle le risque de première espèce est égal au seuil. Pour les lois discrètes ce n’est pas le cas en général ; si nous voulons atteindre le seuil nous sommes obligés d’utiliser des tests aléatoires. Le risque de première espèce dépend en général de \(n\), de \({\cal L}\in{{\mathfrak L}_0}\) et de \(\alpha\) ; il faudrait, en toute rigueur, le noter \( \alpha_{\psi, \alpha, n}({\cal L})\), mais s’il n’y a pas d’ambiguïté nous nous contentons de la notation \(\alpha_{\psi}({\cal L})\) ou \(\alpha({\cal L})\) ou encore \(\alpha(\theta)\), lorsqu’il s’agit d’une hypothèse paramétrique.
Remarque 2. Les tests statistiques sont très conservatifs, c’est-à-dire que, si le nombre d’observations est faible, ils ont tendance à induire la décision «\({\cal H}_0\) est vraie» ; si par contre le nombre d’observations est grand ils ont tendance à induire la décision «\({\cal H}_1\) est vraie». Pour contrecarrer ces tendances, nous proposons la règle empirique suivante permettant de choisir le seuil en fonction du nombre d’observations \(n\) :
| \(n\) | \(n\leq 10\) | \(10 < n \leq 100\) | \(100 < n\) |
| \(\alpha\) | \(0,1\) | \(0,05\) | \(0,01\) |
Définition 2. Nous appelons risque de deuxième espèce du test \(\psi\) associé à la loi \({\cal L}\in{{\mathfrak L}_1}\) le nombre \(\beta_{\psi}\in\lbrack 0\ ;\ 1\rbrack\) tel que :
\[ \beta_{\psi}({\cal L})=1-{\mathbb E}_{\cal L}\lbrack \psi(X_{\bullet})\rbrack=1-P_{\cal L}(\psi(X_{\bullet})=1). \]Nous appelons puissance du test pour la loi \({\cal L}\in{{\mathfrak L}_1}\) le nombre \(pu_{\psi}({\cal L})=1-\beta_{\psi}({\cal L})={\mathbb E}_{\cal L}\lbrack \psi(X_{\bullet})\rbrack\). Lorsque les hypothèses sont décrites par la variation d’un paramètre \(\theta\), alors \(pu_{\psi}({\cal L})=pu_{\psi}(\theta)\) est appelée fonction puissance ou encore courbe d’efficacité.
Interprétation. Le risque \(\beta_{\psi}({\cal L})\) correspond à la probabilité de l’erreur de deuxième espèce, c’est-à-dire celle de décider «\({\cal H}_0\) est vraie» à tort lorsque \({\cal H}_1\) est vraie. C’est, selon notre principe général, la probabilité sous \({\cal H}_1\) du complémentaire de l’événement rare, dont la réalisation impliquera la décision «\({\cal H}_0\) est vraie», ou encore «le test est non significatif». Le nombre \(pu_{\psi}({\cal L})\), pour \({\cal L}\in{{\mathfrak L}_1}\), est la probabilité de «détecter» \({\cal H}_1\) avec le test \(\psi\).
Remarque 3. Le risque de deuxième espèce est aussi très souvent exprimé en pourcentage. Il dépend en général de \(n\), de \({\cal L}\in{{\mathfrak L}_1}\) et de \(\alpha\) ; il faudrait, en toute rigueur, le noter \(\beta_{\psi, \alpha, n}({\cal L})\), mais s’il n’y a pas d’ambiguïté nous nous contentons de la notation \(\beta_{\psi}({\cal L})\) ou \(\beta({\cal L})\) ou encore \(\beta(\theta)\), lorsqu’il s’agit d’une hypothèse paramétrique. Empiriquement, une valeur inférieure à \(20 \%\) est acceptable. Souvent il est difficile, sinon impossible, à évaluer. Dans certains cas cependant, nous pouvons l’approcher asymptotiquement ou par simulation.
Remarque 4. D’une manière générale \(pu_{\psi}({\cal L})={\mathbb E}_{\cal L}\lbrack \psi(X_{\bullet})\rbrack\). Lorsque \({\cal L}\in{{\mathfrak L}_0}\), alors \(pu_{\psi}({\cal L})=\alpha_{\psi}({\cal L})\) ; lorsque \({\cal L}\in{{\mathfrak L}_1}\) alors \(pu_{\psi}({\cal L})=1-\beta_{\psi}({\cal L})\). Dans le cas paramétrique, lorsque \(\theta\in\Theta_0\) la fonction puissance est majorée par \(\alpha\) ; lorsque \(\theta\in\Theta_1\) c’est la puissance proprement dit.
Définition 3. Soit un test fondé sur une statistique. Nous appelons \(p\)-valeur la probabilité d’observer, en supposant que «\({\cal H_0}\) est vraie», des réalisations de cette statistique au moins aussi extrêmes que celles que nous avons observées.
Interprétation. Ce concept a été introduit par Fisher. Il nous indique à partir des observations si, de manière simplifiée, «\({\cal H_0}\) est vraie» est probable ou pas. La \(p-\)valeur permet de prendre une décision sans être obligé de calculer la ou les valeurs critiques. En effet :
- si la \(p-\)valeur est inférieure à \(\alpha\), nous décidons «\({\cal H}_1\) est vraie» ;
- si la \(p-\)valeur est strictement supérieure à \(\alpha\), nous décidons «\({\cal H}_0\) est vraie».
La plupart des logiciels affichent cette \(p-\)valeur comme résultat d’un test. Ainsi il est important d’avoir bien précisé l’alternative. Dans tous les exemples et applications, nous donnerons la ou les valeurs critiques et, lorsque cela sera possible, la \(p-\)valeur.
Définition 4. Lorsque nous sommes dans le cas paramétrique, nous supposons disposer d’un estimateur \(\widehat{\theta}\) convergent et sans biais des paramètres. Alors, si la réalisation \(\widehat{\theta}(x_{\bullet})\) est dans \({\cal H_1}\), nous appelons puissance a posteriori le nombre \(pu_{\psi}(\widehat{\theta}(x_{\bullet}))\).
Interprétation. Lorsque nous décidons que \({\cal H_1}\) est vraie, le risque est égal au seuil et donc très petit ; nous faisons confiance à notre décision. Lorsque nous décidons que \({\cal H_0}\) est vraie, nous ne connaissons pas le risque en général. Si une ou des valeurs particulières des paramètres dans \({\cal H_1}\) nous intéressent et si nous pouvons calculer la puissance en ces points, une grande puissance, de l’ordre de \(80 \%\), nous permet de faire confiance à notre décision. mais si nous n’avons aucun point d’intérêt alors nous pouvons calculer la puissance a posteriori. C’est-à-dire, nous faisons comme si l’estimation \(\widehat{\theta}(x_{\bullet})\) nous donnait la vraie valeur du ou des paramètres et nous calculons la puissance du test à ce point là. Une puissance a posteriori supérieure à \(80 \%\) est rassurante dans le cas d’un test non significatif. Si par contre elle est trop faible, il faudrait éventuellement refaire un échantillon de taille plus grande.
Définition 5. Un test \(\psi\) est appelé sans biais au seuil \(\alpha\) lorsque :
\[ {\mathbb E}_{\cal L}\lbrack \psi(X_{\bullet})\rbrack=\alpha_{\psi}({\cal L})\leq\alpha,\quad \forall{\cal L}\in{\mathfrak L}_0\quad{\it et} \quad \alpha\leq {\mathbb E}_{{\cal L}^{\prime}}\lbrack\psi(X_{\bullet})\rbrack=pu_{\psi}({\cal L}^{\prime})=1-\beta_{\psi}({\cal L}^{\prime}),\quad \forall{\cal L}^{\prime}\in {\mathfrak L}_1. \]Interprétation. Pour un test sans biais au seuil \(\alpha\), le risque de première espèce est majoré par \(\alpha\) ; le risque de deuxième espèce est majoré par \(1-\alpha\) ; il ne peut pas atteindre la valeur \(1\). De manière équivalente, la probabilité de détecter \({\cal H}_1\), c’est-à-dire \(pu({\cal L})\) pour \({\cal L}\in{{\mathfrak L}_1}\), est supérieure à \(\alpha\).
Définition 6. Un test \(\psi\) de seuil \(\alpha\) est plus puissant qu’un test \(\psi^{\prime}\) si :
- \(\alpha_{\psi^{\prime}}({\cal L})\leq \alpha,\quad\forall {\cal L}\in{{\mathfrak L}_0}\) ;
- \(\beta_{\psi}({\cal L})\leq\beta_{\psi^{\prime }}({\cal L})\ \) ou de manière équivalente,
\(pu_{\psi^{\prime}}({\cal L})\leq pu_{\psi}({\cal L})\), \(\quad \forall {\cal L}\in{{\mathfrak L}_1}\).
Un test \(\psi\) est uniformément plus puissant (en abrégé U.P.P.) s’il est plus puissant que tout autre test de même seuil.
Interprétation. Un test U.P.P. nous donne le risque de deuxième espèce le plus petit possible, ce qui est important lorsque le test n’est pas significatif. Ainsi, chaque fois que cela est possible, c’est un tel test qu’il faut mettre en œuvre.
Définition 7. Un test \(\psi\), de seuil \(\alpha\), est appelé convergent lorsque :
\[ \lim_{n\rightarrow +\infty}\beta_{\psi}({\cal L}^{\prime})=0\quad {\it ou}\quad \lim_{n\rightarrow +\infty}pu_{\psi}({\cal L}^{\prime})=1,\quad \forall {\cal L}^{\prime}\in{{\mathfrak L}_1},\quad {\it et}\quad \lim_{n\rightarrow +\infty}\alpha_{\psi}({\cal L})=0,\quad \forall {\cal L}\in{{\mathfrak L}_0}, \]sauf pour les lois \({\cal L}\in{{\mathfrak L}_0}\) telles que \(\alpha_{\psi}({\cal L})=\alpha\).
Interprétation. Pour un test convergent, lorsque la taille de l’échantillon augmente, le risque de deuxième espèce diminue ; c’est-à-dire que la probabilité de commettre une erreur lorsque le test est non significatif tend vers \(0\). Il en est de même pour le risque de première espèce, c’est-à-dire lorsque le test est significatif, sauf pour les lois qui définissent les valeurs critiques. Donc à l’infini il n’induit jamais de décision fausse ; c’est le test idéal.
Remarque 5. C’est la condition sur \(\beta_{\psi}\) qui est la plus importante ; en effet pour l’autre risque nous avons toujours \(\alpha_{\psi}({\cal L})\leq \alpha, \forall {\cal L}\in{{\mathfrak L}_0}\).
Exemple. Soit \(\theta\in {\mathbb R}_+^{\star}\) et \(X\) une v.a. de loi Uniforme \({\cal U}(\rbrack 0\ ;\ \theta\lbrack)\). Nous fixons \(\theta_0\in {\mathbb R}_+^{\star}\) et un seuil \(\alpha\in\rbrack 0\ ;\ 1\lbrack\). Nous observons \(x_{\bullet}=(x_1, \cdots,\ x_n)\) un \(n-\)échantillon de \(X\) et nous nous proposons de tester l’alternative :
Des lois des statistiques d’ordre \(X_{(n)}=\displaystyle\max_{j=1}^nX_j\) et \(X_{(1)}=\displaystyle\min_{j=1}^nX_j\), nous savons que leurs f.r. vérifient :
\[ F_X(t)=tI_{\rbrack 0\ ;\ \theta\lbrack}(t)+I_{\lbrack \theta\ ;\ +\infty\lbrack}(t)\quad \Longrightarrow \quad F_{X_{(n)}}(t)=F_X^n(t),\quad F_{X_{(1)}}(t)=1-(1-F_X(t))^n. \]Nous considérons deux tests \(\psi_1(x_{\bullet})=I_{\rbrack c_1\ ;\ +\infty\lbrack}(x_{(n)})\) et \(\psi_2(x_{\bullet})=I_{\rbrack c_2\ ;\ +\infty\lbrack}(x_{(1)})\). Intuitivement c’est le premier test fondé sur la statistique \(X_{(n)}\), dont les réalisations sont les plus proches du paramètre, qui semble le meilleur. Nous allons le prouver rigoureusement. Pour déterminer les valeurs critiques \(c_1\) et \(c_2\) nous utilisons l’égalité \(\alpha={\mathbb E}_{\theta_0}\lbrack \psi_i(X_{\bullet})\rbrack\) pour \(i=1,\ 2\). Nous en déduisons :
\[ c_1=\theta_0(1-\alpha)^{\frac{1}{n}},\quad c_2=\theta_0(1-\alpha^{\frac{1}{n}}). \]Remarquons que l’inégalité \(1\leq \alpha^{\frac{1}{n}}+(1-\alpha)^{\frac{1}{n}}\) implique \(c_2\leq c_1\). Nous pouvons calculer les fonctions puissances :
\[ pu_{\psi_1}(\theta)=\left(1-(\frac{\theta_0}{\theta})^n(1-\alpha)\right)I_{\rbrack c_1\ ;\ +\infty\lbrack}(\theta), \quad pu_{\psi_2}(\theta)=\left(1-\frac{\theta_0}{\theta}(1-\alpha^{\frac{1}{n}})\right)^n I_{\rbrack c_2\ ;\ +\infty\lbrack}(\theta). \]Nous constatons que ces deux fonctions sont croissantes en \(\theta\). Ainsi nous obtenons aisément, pour \(i=1,\ 2\) :
\[ \theta\leq\theta_0 \Longrightarrow pu_{\psi_i}(\theta)\leq pu_{\psi_i}(\theta_0)=\alpha\quad \text{et}\quad \theta_0 <\theta \Longrightarrow pu_{\psi_i}(\theta)\geq pu_{\psi_i}(\theta_0)=\alpha, \]c’est-à-dire que les deux tests sont de seuil \(\alpha\) et sont sans biais. De plus :
\[ \theta_0 <\theta \Longrightarrow \lim_{n\rightarrow +\infty}pu_{\psi_1}(\theta)=1\quad\text{et}\quad \lim_{n\rightarrow +\infty}pu_{\psi_2}(\theta)=\alpha^{\frac{\theta_0}{\theta}}. \]Si \(\theta < \theta_0\), alors, à partir d’un certain rang, \(\theta < c_1=\theta_0(1-\alpha)^{\frac{1}{n}}\), ce qui implique que \( \alpha_{\psi_1}(\theta)=0\). Bien entendu \(\alpha_{\psi_1}(\theta_0)=\alpha\). Ainsi le test \(\psi_1\) est convergent et le test \(\psi_2\) ne l’est pas. Enfin l’étude du sens de variation de la fonction \(\theta^n(\psi_1(\theta)-\psi_2(\theta))\) nous montre que :
\[ \theta\leq\theta_0 \Longrightarrow pu_{\psi_1}(\theta)\leq pu_{\psi_2}(\theta)\quad \text{et}\quad \theta_0 <\theta \Longrightarrow pu_{\psi_1}(\theta)\geq pu_{\psi_2}(\theta) ; \]Le test \(\psi_2\) est moins puissant que \(\psi_1\). En conclusion c’est bien le test \(\psi_1\) qu’il faut utiliser.
Application numérique. Posons \(\theta_0=1\) ; c’est-à-dire que nous avons l’alternative :
Pour \(n=5\) et \(\alpha=0,1\) les valeurs critiques sont \(\displaystyle c_1=\theta_0(1-\alpha)^{\frac{1}{n}}=0,979484\) et \(\displaystyle c_2=\theta_0(1-\alpha^{\frac{1}{n}})^{\frac{1}{n}}=0,3690427\). Les deux tests sont donc définis par :
\[ \psi_1(x_{\bullet})=I_{\rbrack 0,979\ ;\ +\infty\lbrack}(x_{(5)})\quad\text{et}\quad \psi_2(x_{\bullet})=I_{\rbrack 0,369\ ;\ +\infty\lbrack}(x_{(1)}). \]Les fonctions puissances quant à elles s’écrivent :
\[ pu_{\psi_1}(\theta)=I_{\rbrack 0,979\ ;\ \ +\infty\lbrack}(\theta)\left(1-\dfrac{0,9}{\theta^5}\right)\quad\text{et}\quad pu_{\psi_2}(\theta)=I_{\rbrack 0,369\ ;\ \ +\infty\lbrack}(\theta)\left(1-\dfrac{1-0,1^{0,2}}{\theta}\right)^5. \]Graphique 1. La Fig. 1 ci-dessous représente les courbes des fonctions puissances des deux tests.
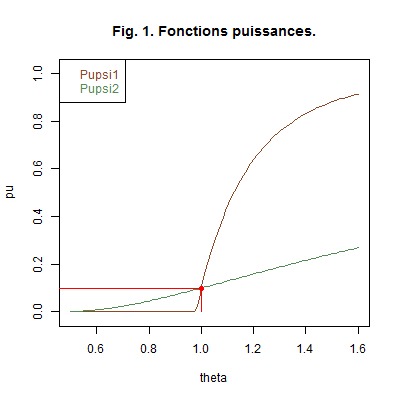
Nous avons marqué en rouge le point de coordonnées \((\theta_0\ ;\ \alpha)\), ce qui nous permet d’illuster les propriétés des deux tests. Nous avons observé :
\[ 0,429\quad 0,134\quad 0,936\quad 0,885\quad 0,774 \]Nous mettons en œuvre le premier test \(\psi_1\). Comme \(\displaystyle x_{(5)}=\max_{j=1}^5 x_j=0,936\leq c_1=0,979\), il s’ensuit que \(\psi_1(x_{\bullet})=0\) ; ainsi notre décision est «\({\cal H_0}=\lbrace \theta\leq 1\rbrace\) est vraie». Remarquons que la \(p-\)valeur est \( P_{\theta_0}(X_{(5)}> 0,936)=1-(\dfrac{0,936}{\theta_0})^5=0,2815786\geq\alpha=0,1 \) ; bien entendu nous prenons la même décision : le test est non significatif. Remarquons que cette décision aurait pu être prise sans le calcul de \(c_1\), mais uniquement avec le calcul de cette dernière probabilité.
Nous savons que \(\widehat{\theta}(X_{\bullet})=\dfrac{n+1}{n}X_{}(n)\) est un estimateur convergent et sans biais de \(\theta\). Comme \(\widehat{\theta}(X_{\bullet})=1,1232\in{\cal H}_1\), nous calculons la puissance a posteriori : \(pu_{\psi_1}(\widehat{\theta}(x_{\bullet}))=1-\dfrac{0,9}{1,1232^5}=0,4965\leq 0,8\) ; ainsi nous en déduisons que nous ne pouvons pas faire confiance à notre décision. Il faudrait, par exemple, augmenter le nombre d’observations.\(\quad \square\)
Haut de la page.