Tests sur deux moyennes indépendantes

7.5.2.a. Tests asymptotiques sur la différence des moyennes de deux v.a. indépendantes - Contre-hypothèses unilatérales.

Nous présentons des tests asymptotiques sur la différence des moyennes théoriques de deux v.a., notées \(X^{(1)}\) et \(X^{(2)}\), indépendantes et de lois inconnues. Ces tests ont des contre-hypothèses unilatérales. Comme pour l’estimation de la différence de deux moyennes théoriques, nous utilisons des méthodes asymptotiques générales, forcément approximatives. C’est pourquoi nous considérons des échantillons de taille au moins \(50\) et nous interprétons les résultats avec réserve.

Nous supposons que \(X^{(1)}\) et \(X^{(2)}\) admettent des variances théoriques inconnues, \({\mathbb V}ar\lbrack X^{(i)}\rbrack=\sigma^2_i<\infty\), et donc des moyennes théoriques \({\mathbb E}\lbrack X^{(i)}\rbrack=\mu_i<\infty\), pour \(i=1,\ 2\). Soit \(X_{\bullet}^{(i)}=(X_1^{(i)},\ \cdots,\ X_{n_i}^{(i)})\) un \(n_i\)-échantillon de \(X^{(i)},\ i=1,\ 2\). Les deux échantillons sont indépendants. Nous considèrons les statistiques :

\(D_m(X_{\bullet}^{(1)}\ ;\ X_{\bullet}^{(2)})=D_m={\overline X}^{(1)}-{\overline X}^{(2)}=\dfrac{1}{n_1}\displaystyle\sum_{j=1}^{n_1}X^{(1)}_j-\dfrac{1}{n_2}\sum_{j=1}^{n_2}X^{(2)}_j\) et
\(S_m^2(X_{\bullet}^{(1)}\ ;\ X_{\bullet}^{(2)})=S_m^2=\dfrac{S_c^2(X_{\bullet}^{(1)})}{n_1}+\dfrac{S_c^2(X_{\bullet}^{(2)})}{n_2}=\dfrac{1}{n_1(n_1-1)}\displaystyle\sum_{j=1}^{n_1}(X^{(1)}_j-{\overline X}^{(1)})^2+ \frac{1}{n_2(n_2-1)}\sum_{j=1}^{n_2}(X^{(2)}_j-{\overline X}^{(2)})^2,\)

la différence des moyennes et la variance de cette différence, empiriques. Nous notons :

\({\mathbb E}\lbrack D_m\rbrack=\mu_1-\mu_2=\delta_m,\quad {\mathbb V}ar\lbrack D_m\rbrack=\dfrac{\sigma^2_1}{n_1}+\dfrac{\sigma^2_2}{n_2}=\sigma^2_m\quad {\rm et} \ \quad {\mathbb E}\lbrack S^2_m\rbrack=\sigma^2_m.\)

Propriété 1. Sous l’hypothèse d’existence des variances \(\sigma_i^2,\ i=1,\ 2,\) nous avons les résultats suivants :

Si \(n_{tot}=n_1+n_2\), la variance \(\sigma_m^2\) est minimale pour \(n_1=n_{tot}\dfrac{\sigma_1}{\sigma_1+\sigma_2}\) et \(n_2=n_{tot}\dfrac{\sigma_2}{\sigma_1+\sigma_2}\).
\(\displaystyle \lim_{n_1,\ n_2\rightarrow +\infty} {\cal L}_{\delta_m,\sigma_m}\Big(\frac{D_m-\delta_m}{\sigma_m}\Big)={\cal N}(0\ ;\ 1),\ \) c’est-à-dire \(\displaystyle \lim_{n_1,\ n_2\rightarrow +\infty}P_{\delta_m, \sigma_m}\left(\frac{D_m-\delta_m}{\sigma_m}\leq t\right)=\Phi(t),\ \forall t\in {\mathbb R}\).
\(S_m\overset{P}{\underset{n_1,\ n_2\rightarrow+\infty}\longrightarrow}\sigma_m\).
\(\displaystyle\lim_{n_1,\ n_2\rightarrow +\infty} {\cal L}_{\delta_m}\left(\frac{D_m-\delta_m}{S_m}\right)={\cal N}(0\ ;\ 1),\ \) c’est-à-dire \(\displaystyle \lim_{n_1,\ n_2\rightarrow +\infty}P_{\delta_m}\left(\frac{D_m-\delta_m}{S_m}\leq t\right)=\Phi(t),\ \forall t\in {\mathbb R}\).

Nous avons noté \({\cal N}(0\ ;\ 1)\) la loi Normale Standard et \(\Phi\) sa f.r..

Le premier résultat a déjà été vu lors de la Propriété 3 de l’estimation de la différence de deux moyennes théoriques ; il est issu d’un calcul direct. Les trois suivants sont fondés sur la condition d’existence de \(\sigma^2_m\), la Propriété 1 de l’estimation de la différence de deux moyennes théoriques, le T.L.C. et la loi Faible des Grands Nombres. \(\ \square\)

Alternative 1a.

Soit \(\delta_0\in{\mathbb R}\) donné et \(\alpha\in \rbrack 0\ ;\ 1\lbrack\) un seuil fixé. Pour tester l’alternative :

\({\cal H}_0^{(1a)}=\lbrace\delta_{m}\leq\delta_0\rbrace\quad\) contre \(\quad{\cal H}_1^{(1a)}=\lbrace \delta_0 < \delta_m\rbrace\),

ainsi que les Alternatives 1a associées, nous considérons le test asymptotique \(\psi^{(1a)}_{\infty}(d_m)=I_{\rbrack c\ ;\ +\infty\lbrack}(d_m)\), où \(c=\delta_0+q_{1-\alpha}\sigma_m\) et le nombre \(q_{1-\alpha}\) est le quantile d’ordre \(1-\alpha\) de la loi \({\cal N}(0\ ;\ 1)\). Ainsi en théorie :

si \(c < d_m\), alors nous décidons «\({\cal H}_1^{(1a)}\) est vraie» ;
si \(d_m \leq c\), alors nous décidons «\({\cal H}_0^{(1a)}\) est vraie».

Les variances étant en général inconnues, si nous avons observé \(S_m=s_m\), le nombre \(c\) peut être estimé par \(\widehat{c}=\delta_0+q_{1-\alpha}s_m\). Ainsi en pratique :

si \(\widehat{c}< d_m\), alors nous décidons «\({\cal H}_1^{(1a)}\) est vraie» ;
si \(d_m \leq \widehat{c}\), alors nous décidons «\({\cal H}_0^{(1a)}\) est vraie».

Remarque 1. Si pour l’utilisateur décider à tort que la différence des moyennes théoriques de deux v.a. de lois inconnues est plus grande qu’une valeur donnée a les conséquences les plus défavorables, c’est sur ce test \(\psi^{(1a)}_{\infty}\) qu’il doit fonder sa démarche. Ce test \(\psi^{(1a)}_{\infty}\) au seuil \(\alpha\) est identique au test \(1-\psi^{(1b)}_{\infty}\), présenté ci-après, au seuil \(1-\alpha.\) Le choix de l’atternative est donc fondamental.

Propriété 2. Le test \(\psi^{(1a)}_{\infty}\) satisfait à :

Pour tout \(\delta_m \leq \delta_0\), nous avons \(\displaystyle\lim_{n_1, n_2\rightarrow +\infty}{\mathbb E}_{\delta_m,\sigma_m}\left\lbrack\psi^{(1a)}_{\infty}(D_m)\right\rbrack\leq \displaystyle\lim_{n_1, n_2\rightarrow +\infty}{\mathbb E}_{\delta_0,\sigma_m}\left\lbrack\psi^{(1a)}_{\infty}(D_m)\right\rbrack=\alpha\) ; le test est asymptotiquement de seuil \(\alpha\).
Pour tout \(\delta_0 < \delta_m\), nous avons \(\alpha\leq\displaystyle\lim_{n_1, n_2\rightarrow +\infty}{\mathbb E}_{\delta_m,\sigma_m}\left\lbrack\psi^{(1a)}_{\infty}(D_m)\right\rbrack\) ; le test est, pour ce seuil, asymptotiquement sans biais.
Une approximation de la fonction puissance asymptotique au point \(\delta_m\) est donnée par :
\(pu_{\psi^{(1a)}_{\infty}}(\delta_m)\approx 1-\Phi\Big(q_{1-\alpha}+\dfrac{\delta_0-\delta_m}{\sigma_m}\Big)\).
Une estimation convergente de cette approximation est donnée par :
\(\widehat {pu}_{\psi^{(1a)}_{\infty}}(\delta_m)\approx 1-\Phi\Big(q_{1-\alpha}+\dfrac{\delta_0-\delta_m}{s_m}\Big)\).

Un calcul simple sur la f.r. de la loi Normale Standard \(\Phi\) et l’appliquation de la Propriété 1, ii. et iii., nous donnent ces résultats.\(\ \square\)

Remarque 2. Si nous avons observé \(D_m=d_m\), alors l’approximation de la puissance a posteriori peut être estimée par :

\(\widehat{pu}_{\psi^{(1a)}_{\infty}}(d_m)\approx 1-\Phi\Big(q_{1-\alpha}+\dfrac{\delta_0-d_m}{s_m}\Big).\)

Remarque 3 La puissance est maximale lorsque la variance de la différence des moyennes est minimale. D’après la Propriété 1, i., en estimant \(\sigma_1\) et \(\sigma_2\) nous pouvons juger a posteriori ce qu’il en est pour la taille des échantillons observés.

Propriété 3. Si nous avons observé \(D_m=d_m\), alors la \(p\)-valeur du test est :

\(p_{val}=1-\Phi\Big(\dfrac{d_m-\delta_0}{\sigma_m}\Big).\)

Ainsi en théorie :

si \(p_{val} < \alpha\), nous décidons «\({\cal H}_1^{(1a)}\) est vraie»
si \(\alpha \leq p_{val}\), nous décidons «\({\cal H}_0^{(1a)}\) est vraie».

L’écart type \(\sigma_m\) étant en général inconnu, nous l’estimons par \(s_m\) et la \(p\)-valeur par :

\(\widehat{p}_{val}=1-\Phi\Big(\dfrac{d_m-\delta_0}{s_m}\Big).\)

Ainsi en pratique :

si \(\widehat{p}_{val} < \alpha\), nous décidons «\({\cal H}_1^{(1a)}\) est vraie»
si \(\alpha \leq \widehat{p}_{val}\), nous décidons «\({\cal H}_0^{(1a)}\) est vraie».

Pour le voir il suffit de montrer qu’en remplaçant \(1-\alpha\) par \(\Phi(q_{1-\alpha})\) dans les inégalités sur la \(p\)-valeur, nous obtenons les mêmes décisions que celles de la définition du test. \(\ \square\)

Remarque 4. Nous avons créé dans R deux procédures. La première Test1aAsym2MoyeInde qui permet de réaliser le test \(\psi^{(1a)}_{\infty}\). La seconde Puis1aAsym2MoyeInde qui permet le calcul d’une estimation de l’approximation de la puissance de ce test.

Exemple 1. Nous considérons les données de Sinistres. Nous notons \(X^{(1)}\) la v.a. «Coût du sinistre avec présence de tiers» et \(X^{(2)}\) la v.a. «Coût du sinistre sans présence de tiers». Nous supposons que ces v.a. admettent une variance théorique et que leurs réalisations sont obtenues de manières indépendantes. Nous nous proposons de tester l’alternative :

\({\cal H}_0^{(1a)}=\lbrace\delta_m=\mu_1-\mu_2\leq 0\rbrace\quad\) contre \(\quad{\cal H}_1^{(1a)}=\lbrace 0 < \delta_m\rbrace\)

Nous utilisons la procédure Test1aAsym2MoyeInde de la Remarque 4 ci-dessus. Après l’avoir compilée («sourcée» dans R), nous l’exécutons en indiquant les données à traiter, \(\delta_0=0\) et le seuil \(\alpha=0,01\) à utiliser, parce que \(n_1=120\) et \(n_2=236\).

Test1aAsym2MoyeInde (Tier1Mont[,2],Tier0Mont[,2],0,0.01), réponse :

Test asymptotique de l'alternative : H^{(1a)}_0={ Delta_m ⩽ 0 } contre H^{(1a)}_1={ 0 < Delta_m }.

Premier échantillon, taille : 120 ; moyenne : 561.6 ; écart type : 666.2 .
Deuxième échantillon, taille : 236 ; moyenne : 268.3 ; écart type : 479 .

Différence des moyennes : 293.3 ; écart type de la différence : 68.34 .

Seuil asymptotique du test : 0.01 ; estimation valeur critique : 159 .

Estimation de la p-valeur : 8.867e-06 .

Décision : «H^{(1a)}_1={ Delta_m > 0 } est vraie».

Estimation des effectifs a posteriori donnant la puissance maximale :
Premier échantillon : 207 ; second échantillon : 149 .

Le test est significatif ; nous décidons que le coût moyen d’un sinistre en présence de tiers est supérieur à celui en absence de tiers. La même conclusion s’obtient en comparant la \(p\)-valeur à \(0,01\). Remarquons que les estimations des effectifs impliquant une puissance asymptotique maximale sont très différentes de celles observées dans la réalité. Nous pouvons estimer une approximation de la puissance asymptotique de ce test aux points \(\delta=200\) et \(\delta=293.3\) par exemple. Après avoir compilé («sourcée» dans R) la procédure correspondante de la Remarque 4 ci-dessus, nous l’exécutons en indiquant les données à traiter, \(\delta_0=0,\ \alpha=0,01\) et \(\delta_m=200\) et une deuxième fois avec \(\delta_m=293,3\).

Puis1aAsym2MoyeInde(Tier1Mont[,2],Tier0Mont[,2],0,0.01,200), réponse : 0.7257,
Puis1aAsym2MoyeInde(Tier1Mont[,2],Tier0Mont[,2],0,0.01,293.3), réponse : 0.9753 .

Nous pouvons également tracer le graphique d’une estimation de l’approximation de la fonction puissance asymptotique du test avec la commande suivante :

plot( function(Mu) Puis1aAsym2MoyeInde(Tier1Mont[,2],Tier0Mont[,2],0,0.01, Delta),-100,350,xlab="mu",
ylab="pu", ylim=c(0,1), main="Fig. 1. Approximation de la puissance\n asymptotique du test 1a.", col="green4"),
segments( x0=c(0,0,293.3,293.3,200,200), y0=c(0,0.01,0,0.9753,0,0.7257), x1=c(0,-100,293.3,-100,200,-100), y1=c(0.01,0.01,0.9753,0.9753,0.7257,0.7257), col="blue"))
points( x=c(0,293.3,200), y=c(0.01,0.9753,0.7257), col="red", pch=".", cex=7), réponse :

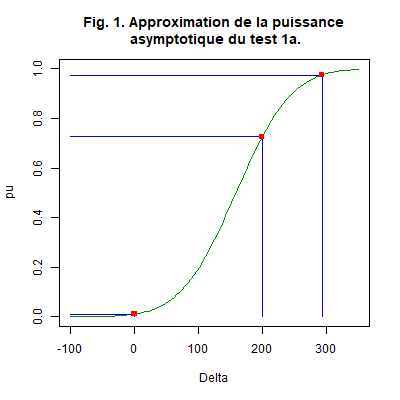
Le test est bien asymptotiquement de seuil \(0,01\) et sans biais. Nous avons marqué en rouge les points de coordonnées \((\delta_0\ ;\ \alpha)=(0\ ;\ 0,01)\), \((200\ ;\ \widehat{pu}(200))\approx(200\ ;\ 0,7257)\) et \((293,3\ ;\ \widehat{pu}(293,3))\approx(293,3\ ;\ 0,9753)\). \(\ \square\)

Alternative 1b.

Soit \(\delta_0\in{\mathbb R}\) donné et \(\alpha\in \rbrack 0\ ;\ 1\lbrack\) un seuil fixé. Pour tester l’alternative :

\({\cal H}_0^{(1b)}=\lbrace\delta_0\leq\delta_m\rbrace\quad\) contre \(\quad{\cal H}_1^{(1b)}=\lbrace \delta_m < \delta_0\rbrace\),

ainsi que les Alternatives 1b associées, nous considérons le test asymptotique \(\psi^{(1b)}_{\infty}(d_m)=I_{\rbrack -\infty\ ;\ c\lbrack}(d_m)\), où \(c=\delta_0+q_{\alpha}\sigma_m\) et le nombre \(q_{\alpha}\) est le quantile d’ordre \(\alpha\) de la loi \({\cal N}(0\ ;\ 1)\). Ainsi en théorie :

si \(d_m < c\), alors nous décidons «\({\cal H}_1^{(1b)}\) est vraie» ;
si \(c \leq d_m\), alors nous décidons «\({\cal H}_0^{(1b)}\) est vraie».

Les variances étant inconnues en général, si nous avons observé \(S_m=s_m\), le nombre \(c\) peut être estimé par \(\widehat{c}=\delta_0+q_{\alpha}s_m\). Ainsi en pratique :

si \(d_m < \widehat{c}\), alors nous décidons «\({\cal H}_1^{(1b)}\) est vraie» ;
si \(\widehat{c} \leq d_m\), alors nous décidons «\({\cal H}_0^{(1b)}\) est vraie».

Remarque 5. Si pour l’utilisateur décider à tort que la différence des moyennes théoriques de deux v.a. de lois inconnues est plus petite qu’une valeur donnée a les conséquences les plus défavorables, c’est sur ce test \(\psi^{(1b)}_{\infty}\) qu’il doit fonder sa démarche. Ce test \(\psi^{(1b)}_{\infty}\) au seuil \(\alpha\) est identique au test \(1-\psi^{(1a)}_{\infty}\), présenté ci-avant, au seuil \(1-\alpha\). Le choix de l’atternative est donc fondamental.

Propriété 4. Le test \(\psi^{(1b)}_{\infty}\) satisfait à :

Pour tout \(\delta_m\), tel que \(\delta_0\leq\delta_m\), nous avons \(\displaystyle\lim_{n_1, n_2\rightarrow +\infty}{\mathbb E}_{\delta_m,\sigma_m}\left\lbrack\psi^{(1b)}_{\infty}\right\rbrack\leq \displaystyle\lim_{n_1, n_2\rightarrow +\infty}{\mathbb E}_{\delta_0,\sigma_m}\left\lbrack\psi^{(1b)}_{\infty}\right\rbrack=\alpha\) ; le test est asymptotiquement de seuil \(\alpha\).
Pour tout \(\delta_m < \delta_0\), nous avons \(\alpha\leq\displaystyle\lim_{n_1, n_2\rightarrow +\infty}{\mathbb E}_{\delta_m,\sigma_m}\left\lbrack\psi^{(1b)}_{\infty}\right\rbrack\) ; le test est, pour ce seuil, asymptotiquement sans biais.
Une approximation de la fonction puissance asymptotique au point \(\delta_m\) est donnée par :
\(pu_{\psi^{(1b)}_{\infty}}(\delta_m)\approx\Phi\Big(q_{\alpha}+\dfrac{\delta_0-\delta_m}{\sigma_m}\Big)\).
Une estimation convergente de cette approximation est donnée par :
\(\widehat {pu}_{\psi^{(1b)}_{\infty}}(\delta_m)\approx\Phi\Big(q_{\alpha}+ \dfrac{\delta_0-\delta_m}{s_m}\Big)\).

Un calcul simple sur la f.r. de la loi Normale Standard \(\Phi\) et l’appliquation de la Propriété 1, nous donnent ces résultats.\(\ \square\)

Notons que la Remarque 3 concernant les effectifs qui impliquent une puissance maximale est encore valable pour ce test.

Remarque 6. Si nous avons observé \(D_m=d_m\), alors une approximation de la puissance asymptotique a posteriori est :

\(pu_{\psi^{(1b)}_{\infty}}(d_m)\approx\Phi\Big(q_{\alpha}+\dfrac{\delta_0-d_m}{\sigma_m}\Big)\)).

Une estimation convergente de cette approximation est :

\(\widehat{pu}_{\psi^{(1b)}_{\infty}}(d_m)\approx\Phi\Big(q_{\alpha}+\dfrac{\delta_0-d_m}{s_m}\Big)\).

Propriété 5. Si nous avons observé \(D_m=d_m\), alors la \(p\)-valeur du test est :

\(p_{val}=\Phi\Big(\dfrac{d_m-\delta_0}{\sigma_m}\Big).\)

Ainsi en théorie :

si \(p_{val} < \alpha\), nous décidons «\({\cal H}_1^{(1a)}\) est vraie»
si \(\alpha \leq p_{val}\), nous décidons «\({\cal H}_0^{(1a)}\) est vraie».

Une estimation convergente de cette \(p\)-valeur est donnée par :

\(\widehat{p}_{val}=\Phi\Big(\dfrac{d_m-\delta_0}{s_m}\Big)\).

Ainsi en pratique :

si \(\widehat{p}_{val} < \alpha\), nous décidons «\({\cal H}_1^{(1a)}\) est vraie»
si \(\alpha \leq \widehat{p}_{val}\), nous décidons «\({\cal H}_0^{(1a)}\) est vraie».

Pour le voir il suffit de montrer qu’en utilisant les propriétés de \(\Phi\) les inégalités sur la \(p\)-valeur conduisent aux décisions données dans la définition du test. \(\ \square\)

Remarque 7. Nous avons créé deux procédures dans R, la première Test1bAsym2MoyeInde qui permet de réaliser le test \(\psi^{(1b)}_{\infty}\), la seconde Puis1bAsym2MoyeInde qui permet le calcul d’une estimation de l’approximation de la puissance de ce test.

Exemple 2. Nous considérons les données de Sinistres. Nous notons \(X^{(1)}\) la v.a. «Coût du sinistre avec une ancienneté de permis de plus de 15 ans» et \(X^{(2)}\) la v.a. «Coût du sinistre avec une ancienneté de permis de moins de 15 ans». Nous supposons que ces v.a. admettent une variance théorique et que leurs réalisations sont obtenues de manières indépendantes. Nous nous proposons de tester l’alternative :

\({\cal H}_0^{(1b)}=\lbrace0\leq \delta_m=\mu_1-\mu_2\rbrace\quad\) contre \(\quad{\cal H}_1^{(1b)}=\lbrace \delta_m < 0\rbrace\)

Nous utilisons la procédure Test1bAsym2MoyeInde de la Remarque 7 ci-dessus. Après l’avoir compilée («sourcée» dans R), nous l’exécutons en indiquant les données à traiter, \(\delta_0=0\) et le seuil \(\alpha=0,01\) à utiliser, parce que \(n_1=214\) et \(n_2=142\).

Test1aAsym2MoyeInde (PermSup15Mont[,2],PermInf15Mont[,2],0,0.01), réponse :
Test asymptotique de l'alternative :H^{(1b)}_0={ 0 ⩽Delta_m} contre H^{(1b)}_1={Delta_m < 0 }.

Premier échantillon, taille : 214 ; moyenne : 296.6 ; écart type : 474.9 .
Deuxième échantillon, taille : 142 ; moyenne : 473.4 ; écart type : 667.8 .

Différence observée : -176.8 ; écart type observé de la différence : 64.76 .

Seuil asymptotique du test : 0.01 ; estimation valeur critique : -150.7 .

Estimation de la p-valeur : 0.003168 .

Décision : «H^{(1b)}_1={ Delta_m < 0 } est vraie».

Estimation des effectifs a posteriori donnant la puissance maximale :
Premier échantillon : 148 ; second échantillon : 208 .

Le test est significatif ; nous décidons que le coût moyen d’un sinistre avec un permis de plus de 15 ans est inférieur à celui avec un permis de moins de 15 ans. La même conclusion s’obtient en comparant la \(p\)-valeur à \(0,01\). Remarquons que les estimations des effectifs impliquant une puissance asymptotique maximale sont très différentes de celles observées dans la réalité. Nous pouvons estimer une approximation de la puissance asymptotique de ce test aux points \(\delta_m=-176\) et \(\delta_m=-250\) par exemple. Après avoir compilé («sourcée» dans R) la procédure correspondante de la Remarque 4 ci-dessus, nous l’exécutons en indiquant les données à traiter, \(\delta_0=0,\ \alpha=0,01\) et \(\delta_m=-176\) et une deuxième fois avec \(\delta_m=-250\).

Puis1bAsym2MoyeInde(PermSup15Mont[,2],PermInf15Mont[,2],0,0.01,-176), réponse : 0.6522,
Puis1bAsym2MoyeInde(PermSup15Mont[,2],PermInf15Mont[,2],0,0.01,-250), réponse : 0.9375 .

Nous pouvons également tracer le graphique d’une estimation de l’approximation de la fonction puissance asymptotique du test avec la commande suivante :

plot( function(Mu) Puis1bAsym2MoyeInde (PermSup15Mont[,2],PermInf15Mont[,2],0,0.01,Delta),-300,100, xlab="Delta",
ylab="pu", ylim=c(0,1), main="Fig. 2. Approximation de la puissance\n asymptotique du test 1b.", col="green4"),
segments( x0=c(0,0,-176,-176,-250,-250), y0=c(0,0.01,0,0.6522,0,0.9375), x1=c(0,-300,-176,-300,-250,-300),
y1=c(0.01,0.01,0.6522,0.6522,0.9375,0.9375), col="blue"))
points( x=c(0,-176,-250), y=c(0.01,0.6522,0.9375), col="red", pch=".", cex=7), réponse :

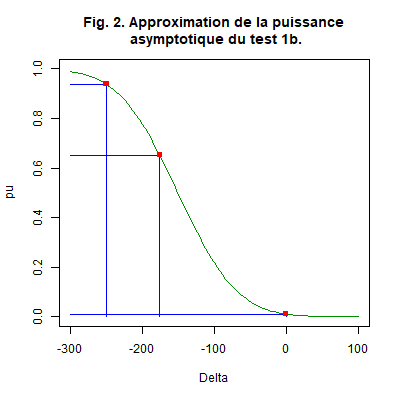
Le test est bien asymptotiquement de seuil \(0,01\) et sans biais. Nous avons marqué en rouge les points de coordonnées \((\delta_0\ ;\ \alpha)=(0\ ;\ 0,01)\), \((-176\ ;\ \widehat{pu}(-176))\approx(-176\ ;\ 0,6522)\) et \((-250\ ;\ \widehat{pu}(-250))\approx(-250\ ;\ 0,9375)\). \(\ \square\)

Haut de la page.

7. Tests classiques d’hypothèses.

7. Tests classiques d’hypothèses.

7.5.2.a. Tests asymptotiques sur la différence des moyennes de deux v.a. indépendantes - Contre-hypothèses unilatérales.