6. Estimation.

Menu principal.
Sommaire général du site.

6. Estimation.

6.0. Généralités sur l’Estimation.
6.1. Propriétés d’un estimateur.
6.2. Méthodes d’estimation.
6.3. Estimation par intervalle.
6.4. Estimation de caractéristiques.
6.5. Estimation d’une f.r. .
6.6. Estimation d’une densité.
6.7. Estimation des paramètres de lois.

Références bibliographiques.
Notations.
Commandes de R.
Index alphabétique.
Index des Mathématiciens - Statisticiens.

---

© Photis NOBELIS, 2009 à .
Ancien Maître de Conférences en Statistique de l'Université Louis Pasteur de Strasbourg.

---

6.6. Estimation d’une fonction de densité.

Il existe plusieurs méthodes d’estimation d’une densité. Parmi les méthodes non paramétriques, citons la méthode des histogrammes, celle des plus proches voisins (que nous développons en Analyse Discriminante et en Classification), celles fondées sur des bases de fonctions, etc. Mais la plus utilisée est la méthode par noyaux dont nous présentons quelques aspects. Elle a été introduite par Rosenblatt et développée par Parzen.

Soit \(X\) une v.a. qui admet une densité \(f_X(t)=f(t)\). Nous nous proposons d’estimer cette dernière à partir de \(X_{\bullet}\) un \(n-\)échantillon de \(X\).

Définition 1. Nous appelons noyau de Parzen toute fonction \(ke(t)\) positive, paire, bornée, satisfaisant aux conditions :

\[ \lim_{t\rightarrow +\infty} t ke(t)= 0\quad {\it et}\quad \int_{-\infty}^{+\infty} ke(t) dt < +\infty. \]

Remarque 1. Les conditions supplémentaires suivantes nous permettront d’obtenir des propriétés usuelles pour les estimateurs de densités :

1. Le noyau est une densité : \(\int_{-\infty}^{+\infty}ke(t)dt=1\) ;
2. Le noyau est de carré intégrable : \(d^2(ke)=\int_{-\infty}^{+\infty}ke(t)^2dt < +\infty\) ;
3. Le noyau admet un moment d’ordre deux : \(\sigma^2(ke)=\int_{-\infty}^{+\infty}t^2ke(t)dt < +\infty\).

Définition 2. Les noyaux les plus utilisés sont :

- Le noyau uniforme : \(ke(t)=\displaystyle\frac{1}{2} I_{\rbrack -1 ; 1\lbrack}(t)\). Il correspond à la densité de la loi Uniforme \({\cal U}(\rbrack -1\ ;\ 1\lbrack)\).
- Le noyau triangulaire : \(ke(t)=(1-\mid t\mid)I_{\rbrack -1 ; 1\lbrack}(t)\). Il correspond à la densité de la loi Triangulaire \({\cal TR}(0)\).
- Le noyau d’Epanechnikov : \(ke(t)=\displaystyle\frac{3}{4}(1-t^2)I_{\rbrack -1 ; 1\lbrack}(t)\).
- Le noyau quartique : \(ke(t)=\displaystyle\frac{15}{16}(1-t^2)^2 I_{\rbrack -1 ; 1\lbrack}(t)\).
- Le noyau circulaire : \(ke(t)=\displaystyle\frac{\pi}{4}\cos(\frac{\pi}{2}t) I_{\rbrack -1 ; 1\lbrack}(t)\).
- Le noyau gaussien : \(ke(t)=\displaystyle\frac{1}{\sqrt{2\pi}} \exp(-\frac{t^2}{2})\). Il correspond à la densité de la loi Normale standard \({\cal N}(0\ ;\ 1)\).

Toutes ces fonctions sont bien des noyaux et satisfont à l’ensemble des conditions de la Remarque 1. En particulier nous avons :

Définition 3. Nous appelons estimateur de Rosenblatt-Parzen ou estimateur à noyau la v.a. :

\[ f^{\star}_n(t)=\frac{1}{nh}\sum_{j=1}^n ke\left(\frac{t-X_j}{h}\right)=\frac{1}{h}{\mathbb E}\left\lbrack ke\left(\frac{t-X_{EM}}{h}\right)\right\rbrack, \]

où \(ke\) est un noyau de Parzen et le nombre \(h=h_n > 0\) est un paramètre de lissage appelé fenêtre. Nous notons également \(f^{\star}_n(t)\) une réalisation de l’estimateur.

Exemple. Nous considérons l’Exemple 4 concernant le dosage d’une substance contenue dans \(n=150\) flacons d’une même production d’une usine pharmaceutique. Nous estimons la densité \(f(t)\) de la v.a. \(X\) «dosage de la substance contenue dans un flacon choisi au hasard dans la production». Nous traçons le graphique des estimations de la densité obtenues avec trois noyaux différents :

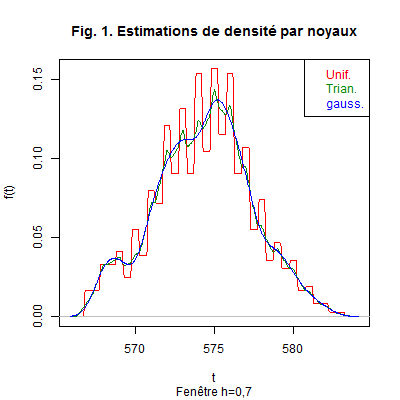
Ce graphique a été obtenu avec les commandes suivantes R :

plot(density(Donnees[,1],bw=.7,adjust=1,kernel="rectangular"),
col="red",xlab="t",ylab="f(t)",main="Fig. 1. Estimations de densité par noyaux",sub="Fenêtre h=0,7");
lines(density(Donnees[,1],bw=.7,adjust=1,kernel="triangular"),col="green4");
lines(density(Donnees[,1],bw=.7,adjust=1,kernel="gaussian"),col="blue");
legend(x="topright",y=NULL,legend=c("Unif.","Trian.","gauss."),text.col=c("red","green4","blue"));

Nous remarquons que, pour le noyau uniforme, l’estimation obtenue est très proche de l’histogramme. La différence réside dans le fait que pour l’histogramme les classes sont fixes à l’opposé de celles de l’estimateur à noyau uniforme qui sont mobiles et centrées sur chaque observation. Ainsi ici deux observations proches peuvent appartenir à deux classes différentes. Naturellement, l’estimation avec le noyau triangulaire comporte des pics, mais celle avec le noyau gaussien est beaucoup plus lisse et régulière. \(\quad \square\)

Remarque 2. Nous avons noté que la f.r. empirique n’est pas continue. Nous pouvons la «lisser» en remplaçant \(I_{\lbrace X_j\leq t\rbrace}(t)\) par \(Ke(t)\), f.r. associée à noyau de Parzen qui soit une densité. En dérivant cette f.r. lisse, notée \(F^{\star}_n(t)\), nous obtenons \(f^{\star}_n(t)\). Ainsi le lien entre l’estimateur de la densité et la loi empirique explique les propriétés asymptotiques données à la suite dans cette page.

Propriété 1. Si le noyau de Parzen est une densité et si \(\displaystyle\lim_{n\longrightarrow +\infty}h_n=0\), alors en tout point \(t_0\), point de continuité de \(f(t)\), nous avons \(\displaystyle\lim_{n\longrightarrow+\infty}{\mathbb E}\left \lbrack f^{\star}_n(t_0)\right\rbrack=f(t_0)\). C’est-à-dire que \(f^{\star}_n(t_0)\) est un estimateur asymptotiquement sans biais de \(f(t_0)\).

Propriété 2. Si les conditions de la Propriété 1 sont satisfaites et si \(\displaystyle\lim_{n\longrightarrow +\infty}nh_n=+\infty\), alors en tout point \(t_0\), point de continuité de \(f(t)\), \(\ f^{\star}_n(t_0)\) est un estimateur convergent de \(f(t_0)\).

Les deux conditions sur \(h_n\) impliquent que cette fenêtre doit tendre vers \(0\), mais avec une certaine lenteur.

Propriété 3. Si les conditions de la Propriété 2 sont satisfaites et si \(d^2(ke) < +\infty\), alors en tout point \(t_0\), point de continuité de \(f(t)\), \(\ f^{\star}_n(t_0)\) est un estimateur asymptotiquement normal de \(f(t_0)\). Nous avons :

\[ \lim_{n\longrightarrow +\infty} {\cal L}\left(\sqrt{nh_n}\frac{f^{\star}_n(t_0)-f(t_0)}{d(ke)\sqrt{f(t_0)}}\right)={\cal N}(0\ ;\ 1). \]

La preuve est fondée sur le Théorème Central Limite de Lindeberg (cf. A. Borovkov (1987)). \(\quad\square\)

Exemple. Nous revenons à l’Exemple 4 concernant le dosage d’une substance contenue dans \(n=150\) flacons. Nous estimons la densité \(f(t)\) avec le noyau d’Epanechnikov, en créant et en affectant celle-ci à l’objet de R que nous nommons fn :

fn=(density(Donnees[,1],bw=.7,adjust=1,kernel="epanecnikov")

Cet objet contient :

fn, réponse :

summary(fn), réponse :

Nous avons ainsi un résumé de la distribution. Remarquons que, par défaut, 512 valeurs de la densité ont été estimées et affectées aux vecteurs fn$x et fn$y. Nous avons, par exemple, la deux cent cinquante et unième estimation :

fn$x[251], réponse : 574.8041

fn$y[251], réponse : 0.1328983

Nous construisons avec ces éléments le graphique suivant :

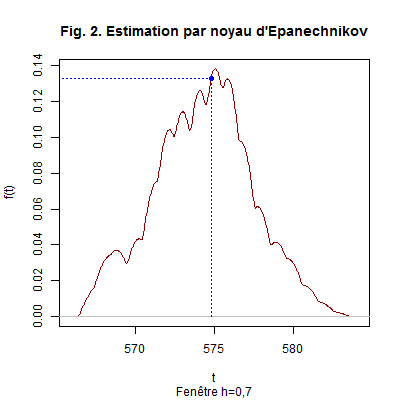
Nous avons utilisé la commande suivante :

plot(fn,col="darkred",xlab="t",ylab="f(t)",
main="Fig. 2. Estimation par noyau d'Epanechnikov",sub="Fenêtre h=0,7");
x0=c(574.8,574.8);y0=c(0,0.1329);x1=c(574.8,0);y1=c(0.1329,0.1329);
segments(x0,y0,x1,y1,lty="dotted",col="blue");
points(x=574.8,y=0.1329,col="blue",pch=16);

Nous en déduisons l’estimation \(f^{\star}_n(574,8041)=0,1328983\). En admettant que toutes les conditions soient satisfaites, c’est la réalisation d’un estimateur de \(f(574,8041)\) qui est convergent, asymptotiquement sans biais et normal. \(\quad\square\)

Propriété 4. Si les conditions de la Propriété 3 sont satisfaites et si \(d^2(ke) < +\infty\), \(\sigma^2(ke) < +\infty\) et \(f(t)\) admet une dérivée seconde de carré intégrable ( i.e. \(\tau^2(f)=\int_{-\infty}^{+\infty}(f^{\prime\prime}(t))^2dt < +\infty\)), alors la fenêtre qui rend minimun l’écart quadratique moyen entre \(f^{\star}_n(t)\) et \(f(t)\) ( i.e. \(\int_{-\infty}^{+\infty}{\mathbb E}\lbrack (f^{\star}_n(t)-f(t))^2\rbrack dt\)) est :

\[ h_n=\left(\frac{d^2(ke)}{n\sigma^4(ke)\tau^2(f)}\right)^{\displaystyle\frac{1}{5}}. \]

Remarque 3. Le résultat précédent ne présente qu’un intérêt théorique, en particulier pour la vitesse de convergence de l’estimateur. En pratique, puisque \(f(t)\) est inconnue, la quantité \(\tau^2(f)\) l’est aussi. Concrètement l’utilisateur choisit \(h_n\) empiriquement, en fonction des objectifs de l’estimation.

Exemple. Nous revenons à l’Exemple 4 concernant le dosage d’une substance contenue dans \(n=150\) flacons. Nous estimons la densité \(f(t)\) avec le noyau d’Epanechnikov, en utilisant trois fenêtres différentes :

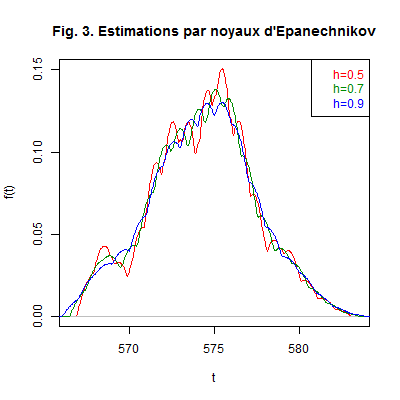
Ce graphique a été obtenu avec les commandes suivantes R :

plot(density(Donnees[,1],bw=.5,adjust=1,kernel="epanechnikov"),
col="red",xlab="t",ylab="f(t)",main="Fig. 3. Estimations par noyaux d'Epanechnikov");
lines(density(Donnees[,1],bw=.7, adjust=1,kernel="epanechnikov"),col="green4");
lines(density(Donnees[,1],bw=.9,adjust=1,kernel="epanechnikov"),col="blue");
legend(x="topright",y=NULL,legend=c("h=0.5","h=0.7","h=0.9"),text.col=c("red","green4","blue"));

Nous constatons que la densité estimée est d’autant plus lisse que la fenêtre est grande. En effet lorsque cette dernière est petite, dans chaque intervalle il y a peu d’observations permettant au noyau de lisser l’estimation de la densité. \(\quad\square\)

Propriété 5. Si les conditions de la Propriété 3 sont satisfaites, alors en tout point \(t_0\), point de continuité de \(f(t)\), un intervalle de confiance asymptotique de \(f(t_0)\) est donné par :

\[ I_{conf}^{\infty}(f(t_0) ;\ \alpha ;\ x_{\bullet})=\left\lbrack f^{\star}_n(t_0) + \frac{c^2d^2(ke)}{2nh_n}(1-\sqrt{A}) ;\ f^{\star}_n(t_0) + \frac{c^2d^2(ke)}{2nh_n}(1+\sqrt{A})\right\rbrack, \]

où \(c\) est le quantile d’ordre \(1-\displaystyle\frac{\alpha}{2}\) de la loi Normale standard et \(A=1+\displaystyle\frac{4nh_n}{c^2d^2(ke)}f^{\star}_n(t_0)\).

De la Propriété 3, nous déduisons :

\[ \lim_{n\longrightarrow +\infty} P\left(\sqrt{nh_n}\frac{\mid f^{\star}_n(t_0)-f(t_0)\mid}{d(ke)\sqrt{f(t_0)}} < c\right)=1-\alpha. \]

La résolution de l’inéquation en \(f(t_0)\) nous donne le résultat. \(\quad\square\)

Exemple. Nous reprenons l’Exemple 4 concernant le dosage d’une substance contenue dans \(n=150\) flacons. En admettant que toutes les conditions soient satisfaites, nous déterminons un intervalle asymptotique de confiance de \(f(574,8041)\). Nous savons que pour \(\alpha=0,05\), la loi Normale standard nous donne \(c=1,96\). Voici les calculs dans R :

A=1+0.1328983*(4*150*0.7/(1.96^2*0.6))
A, réponse : 25.21616
c1=0.1328983+(1.96^2*0.6)/(2*150*0.7)*(1-sqrt(A))
c2=0.1328983+(1.96^2*0.6)/(2*150*0.7)*(1+sqrt(A))
c1, réponse : 0.08875755
c2, réponse : 0.198991

L’intervalle de confiance asymptotique au seuil de \(0,05\) de \(f(574,8041)\) est :

\[ I_{conf}^{\infty}(f(574,8041) ;\ 0,05 ;\ x_{\bullet})=\left\lbrack 0,08875755\ ;\ 0,198991\right\rbrack. \]

Notons que l’amplitude de cet intervalle n’est pas uniforme mais dépend de l’estimation de \(f(t_0)\). \(\quad\square\)

Haut de la page.