Estimation d’une fonction de répartition.

6.5. Estimation d’une fonction de répartition.

Soit \(X\) une v.a. et \(F(t)=F_X(t)=P(X\leq t)\) sa f.r. . Nous nous proposons d’estimer cette fonction à l’aide de \(X_{\bullet}\), un \(n-\)échantillon de \(X\). Si la loi de \(X\) fait partie d’une famille de lois qui dépendent d’un certain nombre de paramètres, il suffit d’estimer ces paramètres (comme décrit dans les pages correspondantes) pour en déduire une estimation de la f.r. ; c’est une méthode paramètrique. Ici nous présentons une démarche non paramétrique, c’est-à-dire qu’elle ne dépend d’aucun paramètre et peut être utilisée en général.

Définition 1. Soit \(X_{(\bullet)}=(X_{(1)},\ X_{(2)},\ \cdots,\ X_{(n)})\) l’échantillon ordonné associé à \(X_{\bullet}\). Nous appelons fonction de répartition empirique associée à cet échantillon, la fonction \(F_n(t)\) définie pour \(t\in{\mathbb R}\) par :

\[ F_{n}(t)=F_{X_{(\bullet)}}(t)=F_{EM}(t)=\frac{1}{n}\sum_{i=1}^n I_{\lbrace X_i\leq t\rbrace}=\frac{1}{n}\sharp (\lbrace X_i\leq t\rbrace)=\cases{ 0 \quad {\rm si} &\( t < X_{(1)}, \)\cr \displaystyle\frac{i}{n} \quad {\rm si} & \( X_{(i)} \leq t < X_{(i+1)}\),\cr 1 \quad {\rm si} &\( X_{(n)} \leq t\), } \]

où \(\sharp(A)\) désigne le nombre d’éléments de l’ensemble \(A\). Nous notons également \(F_n(t)=F_{x_{(\bullet)}}(t)=F_{em}(t)\) une réalisation de cette v.a.. Nous avons indiqué les notations habituelles de cette fonction.

Remarque 1. Nous constatons que la fonction de répartition ainsi définie possède un graphe en escalier, avec un premier palier à l’ordonnée \(0\), un dernier palier à l’ordonnée \(1\) et les paliers intermédiaires à des ordonnées correspondant aux fréquences cumulées associées.

Exemple. Nous considérons l’Exemple 2 concernant la durée de vie d’un équipement. Les 50 observations sont enregistrées sous R dans le tableau Donnees. Celles-ci, classées dans l’ordre croissant, sont :

sort(Donnees[,1]), réponse :
[1] 2.51 2.52 2.54 2.61 2.61 2.61 2.62 2.66 2.66 2.67 2.68 2.68 2.70 2.71 2.71
[16] 2.71 2.71 2.74 2.74 2.75 2.77 2.78 2.79 2.86 2.92 2.96 2.99 3.03 3.03 3.03
[31] 3.04 3.04 3.05 3.05 3.05 3.11 3.14 3.27 3.28 3.32 3.38 3.47 3.72 3.74 3.75
[46] 3.91 4.51 5.51 5.59 6.21

Nous créons la f.r. empirique avec la commande : Fn=ecdf(Donnees[,1]). Le contenu de cet objet et un résumé de la distribution sont :

Fn, réponse :
Empirical CDF
Call: ecdf(X)
x[1:37] = 2.51, 2.52, 2.54, ..., 5.59, 6.21

summary(Fn), réponse :
Empirical CDF: 37 unique values with summary
Min. 1st Qu. Median Mean 3rd Qu. Max.
2.510 2.710 2.990 3.265 3.380 6.210

Nous remarquons qu’il contient entre autres la suite des observations sans ex æquo. Nous constatons, avec la différence entre la médiane et d’une part la moyenne et d’autre part les quartiles, qu’ il y a une forte asymétrie gauche. Nous pouvons également calculer la valeur de la f.r. en un point quelconque, par exemple :

Fn(3.6), réponse : 0.84.

Nous constatons qu’il y a effectivement \(42\) observations qui sont inférieures à \(3,6\). Nous pouvons également tracer le graphique de \(F_n\) avec la commande :

plot(Fn, ylab="Fréquences", xlab="Arrêts", main="Fonction de répartition empirique", col="darkred", col.01line="magenta")

Réponse :

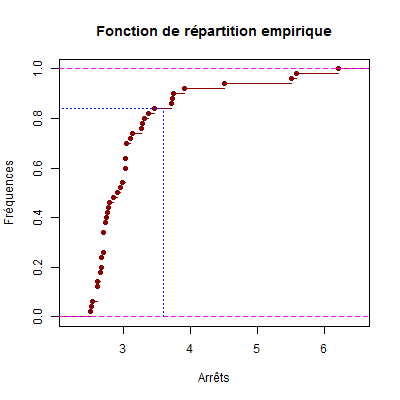
La fenêtre graphique étant ouverte, nous visualisons le fait que \(F_n(3,6)=0,84\) avec les commandes :

x0 = c(3.6,3.6); y0 = c(0,Fn(3.6)); x1 = c(3.6,0); y1 = c(Fn(3.6),Fn(3.6)); segments(x0, y0, x1, y1, lty="dotted", col="blue")

Cette f.r. empirique croît d’abord très rapidement puis beaucoup plus lentement. Ainsi nous retrouvons la forte asymétrie gauche. \(\quad\square\)

Soit \(X\) une v.a. et \(F(t)\) sa f.r. . Nous fixons \(t_0\in{\mathbb R}\) et nous estimons \(F(t_0)\). Concrètement, cette dernière quantité est la proportion théorique des observations qui seront inférieures à \(t_0\). Nous allons utiliser les résultats présentés pour l’estimation d’une proportion théorique ceux pour l’estimation du paramètre d’une loi de Bernoulli.

Propriété 1. La loi de statistique \(nF_n(t_0)=nF_{X_{\bullet}}(t_0)\) est une loi Binomiale \({\cal B}(n\ ;\ F(t_0))\). De plus \(F_n(t_0)\) est un estimateur convergent, sans biais et asymptotiquement normal de \(F(t_0)\). Nous avons :

\[ {\mathbb E}\lbrack F_n(t_0)\rbrack=F(t_0),\quad {\mathbb V}ar\lbrack F_n(t_0)\rbrack=\displaystyle\frac{F(t_0)(1-F(t_0))}{n} \]

\[ \lim_{n\rightarrow +\infty} {\cal L}\left(\sqrt{n}\frac{F_n(t_0)-F(t_0)}{\sqrt{F(t_0)(1-F(t_0))}}\right)={\cal N}(0\ ;\ 1). \]

Propriété 2. Un intervalle de confiance de \(F(t_0)\), au seuil \(\alpha\), est donné par :

\[ I_{conf}(F(t_0)\ ;\ \alpha\ ;\ X_{\bullet})=\lbrack \underline{p}(X_{\bullet})\ ;\ \overline{p}(X_{\bullet})\rbrack, \]

où \(\underline{p}(X_{\bullet})\) (resp. \(\overline{p}(X_{\bullet})\)) est le plus petit (resp. grand) paramètre \(p\) tel que :

\[ nF_n(t_0)\in I_{pred}({\cal B}(n\ ;\ p)\ ;\ \alpha), \]

intervalle de prédiction d’une loi Binomiale de paramètres \(n\) et \(p\).

Propriété 3. Un intervalle de confiance asymptotique de \(F(t_0)\), au seuil \(\alpha\) est donné par :

\[ I_{conf}^{\infty}(F(t_0)\ ;\ \alpha\ ;\ X_{\bullet})=\Big\lbrack \frac{1}{n+c^2}\Big (nF_n(t_0)+\frac{c^2}{2}-c\sqrt{nF_n(t_0)(1-F_n(t_0))+\frac{c^2}{4}}\Big)\ ; \] \[ \frac{1}{n+c^2}\Big (nF_n(t_0)+\frac{c^2}{2}+c\sqrt{nF_n(t_0)(1-F_n(t_0))+\frac{c^2}{4}}\Big)\Big\rbrack. \]

où \(c\) est le quantile d’ordre \(\displaystyle 1-\frac{\alpha}{2}\) de la loi Normale standard \({\cal N}(0\ ;\ 1)\).

Toutes ces propriétés sont des conséquences directes du fait que :

\[ nF_{n}(t_0)=\sum_{i=1}^n I_{\lbrace X_i\leq t_0\rbrace}. \]

Nous reconnaissons la définition des v.a. suivant une loi Binomiale. \(\quad\square\)

Exemple 1. Nous revenons à l’exemple des durées d’un équipement traité ci-dessus. Nous estimons \(F(3,6)\). Après avoir compilé («sourcé») dans l’environnement de travail de R les procédures EstimaProporExact, EstimaProporAsymNormale, nous les appliquons à notre exemple en indiquant le nombre d’observations qui sont inférieures à \(3,6\), le nombre total d’observations \(50\) et le seuil de l’intervalle \(0,05\). Voici les résultats :

EstimaProporExact(42,50,0.05), réponse :
Estimation ponctuelle de la proportion théorique : 0.84
Intervalle de confiance de la proportion théorique au seuil de 5 % :
[ 0.7116 ; 0.9250 ]

EstimaProporAsymNormale(42,50,0.05)
Estimation ponctuelle de la proportion théorique : 0.84
Intervalle de confiance asymptotique avec la loi Normale
de la proportion théorique au seuil de 5 % :
[ 0.7148578 ; 0.9166258 ]

Interprétation. Les deux intervalles sont à peu près les mêmes, notons cependant leur très grande amplitude. Ainsi une estimation ponctuelle de \(F(3,6)\) est \(0,84\) et un intervalle de confiance au seuil de \(0,05\) est donné par :

\[ I_{conf}(F(3.6)\ ;\ 0,05\ ;\ X_{\bullet})=\lbrack 0,712\ ;\ 0,925\rbrack. \]

Pour affiner l’estimation, il faudrait peut-être augmenter la taille de l’échantillon. \(\quad\square\)

En fait nous avons une convergence presque sûre uniforme et, dans certains cas, une convergence en loi. Cette dernière va nous permettre de construire des intervalles de confiance dont l’amplitude ne dépend pas du point \(t_0\) où \(F\) est étudiée, c’est-à-dire que nous allons obtenir une région de confiance globale de \(F\).

Propriété 4. (Glivenko - Cantelli) Soit \(X\) une v.a., \(F(t)\) sa f.r. et \(X_{\bullet}\) un \(n-\)échantillon. Alors

\[ D_n(X_{\bullet})=\sup_{t\in {\mathbb R}}\mid F_n(t) - F(t)\mid \overset{p.s.}{\underset{n\rightarrow+\infty}\longrightarrow}0. \]

Propriété 5. (Kolmogorov) Soit \(X\) une v.a., \(F(t)\) sa f.r. et \(X_{\bullet}\) un \(n-\)échantillon. Alors si \(F(t)\) est une fonction continue nous avons :

\[ P({\sqrt n}D_n(X_{\bullet})\leq s){\underset{n\rightarrow+\infty}\longrightarrow} Ko(s)=\cases{ 0 \quad {\rm si} & \( s\leq 0,\) \cr \displaystyle 1+2\sum_{k=1}^{+\infty}(-1)^k\exp(-2k^2s^2) \quad {\rm si} & \( 0 < s\) }. \]

La fonction \(Ko(s)\) est appelée fonction de Kolmogorov.

Les preuves de ces propriétés sont difficiles et nécessitent des connaissances en théorie des probabilités et processus aléatoires. Il est remarquable que la fonction de Kolmogorov ne dépend pas de \(F(t)\). Nous avons ainsi la région de confiance asymptoptique suivante :

Propriété 6. Soit \(X\) une v.a., \(F(t)\) sa f.r. supposée continue et \(X_{\bullet}\) un \(n-\)échantillon. Alors une région de confiance asymptotique de \(F\) est donné par :

\[ I_{conf}^{\infty}(F\ ;\ \alpha\ ;\ X_{\bullet})=\Big\lbrack F_n-\frac{c}{\sqrt {n}} ;\ F_n+\frac{c}{\sqrt {n}}\Big\rbrack, \]

où \(Ko(c)=1-\alpha\). De plus, pour tout \(t\in{\mathbb R}\), nous avons :

\[ I_{conf}^{\infty}(F(t)\ ;\ \beta\ ;\ X_{\bullet})=\Big\lbrack F_n(t)-\frac{c}{\sqrt {n}} ;\ F_n(t)+\frac{c}{\sqrt {n}}\Big\rbrack, \]

avec \(\beta\leq \alpha\).

Nous notons que l’amplitude de l’intervalle est la même pour tout \(t\in{\mathbb R}\). Cet intervalle asymptotique est plus général ; mais son amplitude est plus large que celle de l’intervalle de la propriété 3 ci-dessus. Ceci est dû au fait que le seuil est faible ou, ce qui est équivalent, que la confiance est supérieure.

Exemple 1. Nous revenons à l’exemple des durées d’un équipement traité ci-dessus. Bien entendu la f.r. de la v.a. «Durée» est continue. Nous avons créé la procédure Kolmogorov qui permet de calculer les valeurs de cette fonction. Ainsi après l’avoir compilée («sourcée») dans l’environnement de travail, nous avons par exemple :

Kolmogorov(1.3581), réponse : 0.9500004

De la propriété précédente nous pouvons construire un intervalle de confiance asymptotique au seuil de \(5 \%\) de \(F\) :

\[ I_{conf}^{\infty}(F\ ;\ 0.05\ ;\ x_{\bullet})=\Big\lbrack F_n-\frac{1.3581}{\sqrt {50}} ;\ F_n+\frac{1.3581}{\sqrt {50}}\Big\rbrack=\Big\lbrack F_n-0,19210\ ;\ F_n+0,19210\Big\rbrack. \]

En particulier au point \(t=3,6\) nous avons :

\[ I_{conf}^{\infty}(F(3,6)\ ;\ \beta\ ;\ x_{\bullet})=\Big\lbrack 0,64794\ ;\ 0,93206\Big\rbrack, \]

avec \(\beta\leq 0,05\). Notons que ce nous avons gagné en généralité, nous l’avons perdu en amplitude.

Haut de la page.

6. Estimation.

6. Estimation.

6.5. Estimation d’une fonction de répartition.