Histogramme.

3.3. Variable continue - histogramme.

Nous donnons la représentation graphique la plus utilisée pour les variables continues.

Définition 1. Considérons la distribution \(Dist(x_{\bullet})=\lbrace (c_1,\ n_1),\ \cdots ,\ (c_r,\ n_r)\rbrace\) associée à un échantillon d’une variable continue. Nous construisons un graphique des fréquences de la manière suivante. Nous reportons les classes sur l’axe des abscisses et, au-dessus de chacune d’elles, nous traçons un rectangle dont l’aire est proportionnelle à la fréquence \(f_i\) associée. Ce graphique est appelé l’histogramme des fréquences.

Interprétation. L’aire des rectangles nous permet de repérer immédiatement les classes les plus ou les moins fréquentes. Nous pouvons également comparer visuellement des classes par leurs fréquences. L’allure de l’histogramme nous donne une idée sur la forme de la distribution.

Remarque. Si les classes sont de même amplitude, nous pouvons tracer l’histogramme en prenant comme hauteur, soit la fréquence, soit directement l’effectif associé. Ce choix permet d’obtenir des aires qui sont alors proportionnelles aux fréquences respectives ; le coefficient de proportionnalité est égal à l’amplitude commune ou l’amplitude commune multipliée par \(n\) respectivement. Par contre lorsque les amplitudes sont différentes cette démarche n’est plus possible et il faut calculer la hauteur de chaque rectangle individuellement, ce qui est, très souvent, source d’erreurs.

Lorsque la taille de l’échantillon tend vers l’infini, des lois de grands nombres apparaissent. L’histogramme tend vers la fonction de densité.

Application 1. Nous reprenons l’exemple des Sinistres. Nous construisons un histogramme pour la variable MONT, coût en euros du sinistre (septième colonne du tableau des données), avec la commande suivante :

hist (Donnees[,7], breaks ="Sturges", freq =FALSE, right =TRUE, include.lowest =TRUE,
col ="cyan", border ="blue", xlab ="Coûts en euros", ylab ="Densités",
main ="Fig. 1 : Histogramme des coûts des sinistres");

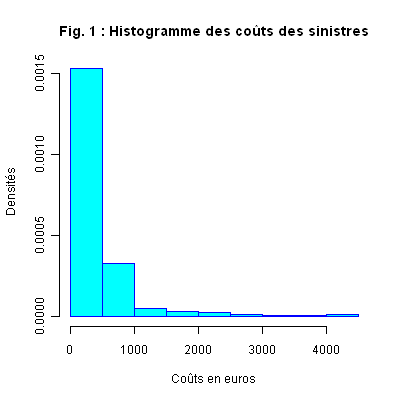
Remarquons les options right=TRUE, include.lowest=TRUE qui permettent d’obtenir les extrémités des classes comme elles sont spécifiées dans la définition. L’option breaks="Sturges" permet de choisir un nombre de classes selon la règle de Sturges. Mais R propose d’autres choix pour les classes, en particulier l’utilisateur peut définir ses propres classes.

Interprétation. Nous constatons une très forte asymétrie de la distribution. Pour la «régulariser» nous pouvons tracer l’histogramme des logarithmes des coûts.

hist (log (Donnees[,7], exp (1)), breaks ="Sturges", freq =FALSE, right =TRUE,
include.lowest =TRUE, col ="bisque1", border ="red",
xlab ="Logarithmes des coûts en euros",
ylab ="Densités",
main ="Fig. 2 : Histogramme des log coûts des sinistres");

Interprétation. Nous constatons une forme de distribution presque «en cloche», ce qui nous fait penser éventuellement à une loi Log-Normale comme distribution théorique pour MONT.

Haut de la page.

3. Descriptions graphiques.

3. Descriptions graphiques.

3.3. Variable continue - histogramme.