Boîte à moustaches.

3.5. Graphique boîte à moustaches.

Ce type de diagramme a été créé en 1977 par Tukey.

Définition 1. Considérons un échantillon $ x_{\bullet}$. Le graphique boîte à moustaches est constitué de deux axes : un axe (en abscisse par exemple) avec une échelle numérique, qui correspond à la variable observée, et un axe (en ordonnée par exemple) sans aucune échelle. Un segment vertical, d’une largeur arbitraire, est tracé en regard de la médiane en général ou de tout autre paramètre de tendance centrale ; un intervalle de confiance peut être matérialisé autour de ce paramètre. Puis un rectangle, la boîte, est reporté avec une largeur légèrement inférieure ou supérieure à celle du segment de la médiane et dont les côtés droit et gauche correspondent respectivement aux quartiles $Q_{0,75}(x_{\bullet})$ et $Q_{0,25}(x_{\bullet})$. Enfin deux segments horizontaux, les moustaches, sont tracés vers l’extérieur du rectangle, joignant :

- le milieu du côté droit à la plus grande observation inférieure ou égale à

\[ Q_{0,75}(x_{\bullet}) + 1,5 IQR(x_{\bullet}), \]

- le milieu du côté gauche à la plus petite observation supérieure ou égale à

\[ Q_{0,25}(x_{\bullet}) - 1,5 IQR(x_{\bullet}). \]

Les extrémités d’une moustache s’appellent valeurs adjacentes, supérieure et inférieure respectivement.

Interprétation. D’une création relativement récente, ce type de graphique permet d’observer le sens de la répartition des valeurs, la position de la valeur médiane et la dispersion des données. Le rectangle correspond à l’intervalle contenant la moitié des observations. Lorsqu’une observation se trouve au-delà des valeurs adjacentes, elle peut être considérée comme extrême. Il faut vérifier son exactitude et éventuellement l’omettre.

Remarque. Plusieurs échantillons peuvent être représentés côte à côte. Sur l’axe sans échelle, nous reportons les attributs qualitatifs caractérisant ces échantillons et nous traçons une boîte à moustaches pour chaque échantillon. Ce diagramme permet de comparer les échantillons visuellement et simplement.

Application 1. Nous reprenons l’exemple des Sinistres. Nous construisons une boîte à moustaches pour la variable AGE du conducteur (cinquième colonne du tableau des donnés), avec la commande suivante :

Boite= boxplot (Donnees[,5], range =1.5, notch =TRUE, outlier =TRUE, plot =TRUE,
border ="chocolate4", col ="gold", horizontal =TRUE,
main ="Fig. 1 : Age du conducteur.");

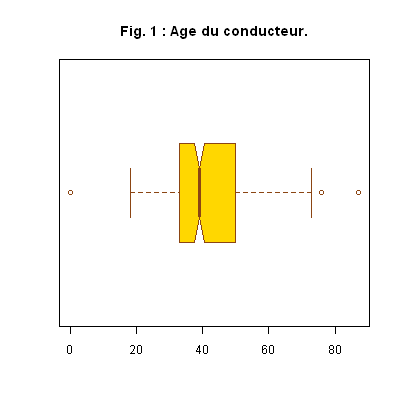
La commande précédente a non seulement créé le graphique, mais également un objet que nous avons nommé «Boite». Nous avons posé la longueur des moustaches égale à 1.5 fois l’$IQR$ ; un intervalle de confiance de la médiane à été visualisé sous forme d’encoches ; nous avons également tracé les valeurs extrêmes. Les sous-objets de l’objet Boite sont :

summary(Boite) ; réponse de R :

	Length	Class	Mode
stats	5	integer	numeric
n	1	-none-	numeric
conf	2	-none-	numeric
out	3	-none-	numeric
group	3	-none-	numeric
names	1	-none-	character

Le contenu de chaque sous-objet est :

Boite$stats ; réponse de R :

	[,1]
[1,]	$18$
[2,]	$33$
[3,]	$39$
[4,]	$50$
[5,]	$73$

Ce sont, respectivement, la valeur adjacente à gauche, le premier quartile, la médiane, le troisième quartile et la valeur adjacente à droite. Ce sont les cinq points qui résument la distribution en non paramétrique.

Boite$n ; réponse de R : $356$.

Boite$conf ; réponse de R :

	[,1]
[1,]	$37.57642$
[2,]	$40.42358$

Ce sont les bornes de l’intervalle de confiance de la médiane, obtenues en ajoutant à celle-ci $ \pm 1,58\displaystyle\frac{IQR(x_{\bullet})}{\sqrt{n}}$. Dans l’étude des intervalles de confiance, nous reviendrons sur cette formule

Boite$out ; réponse de R : $87\quad 0\quad 76$.

Ce sont les valeurs extrêmes. Les deux derniers sous-objets donnent les numéros et les noms des boîtes, lorsqu’il y en a plusieurs.

Interprétation. Nous constatons une forte asymétrie droite. La valeur de la médiane semble connue avec précision : la moitié des conducteurs sont âgés de moins de $39$ ans et l’autre moitié des conducteurs ont un âge supérieur à $39$ ans. Il y a trois observations dont il faut vérifier l’exactitude.

Haut de la page.

3. Descriptions graphiques.

3. Descriptions graphiques.

3.5. Graphique boîte à moustaches.