Graphique des quantiles.

3.6. Graphique des quantiles.

Un graphique des quantiles permet de comparer visuellement soit une distibution observée avec une distribution théorique, soit deux distributions observées. Un tel graphique peut nous aider à choisir une loi pour ajuster à nos observations.

Définition 1. Nous appelons graphique des quantiles ou Q-graphique d’un échantillon observé \(x_{\bullet}\) et d’une distribution théorique, le graphique constitué des points dont les coordonnées sont définies de la manière suivante :

- En abcisse nous reportons l’échantillon ordonné \(x_{(\bullet)}\).

- En ordonnée nous reportons les quantiles de la distributions théorique à comparer, ayant les mêmes fréquences cumulées corrigées que celles des \(x_{(1)},\ x_{(2)},\ \cdots ,\ x_{(n)}\).

Interprétation. En théorie, si les observations sont issues de la loi théorique ci-dessus, alors les points du graphique doivent se situer le long de la première bissectrice. En pratique, à l’exception de quelques points extrêmes, la plupart des autres points doivent se situer autour de cette droite.

Remarque. Lorsqu’il s’agit de comparer deux échantillons, le principe de construction et l’interprétation sont analogues.

Remarque. La fréquence corrigée de \(x_{(i)}\), par exemple, est calculée selon l’expression :

\[ f_{c,i}=\frac{rg(x_{(i)})-a}{n+(1-2a)}; \]

L’expression \(rg(x_{(i)})\) désigne le rang moyen de l’observation \(x_{(i)}\) ; elle est égale soit à \(i\) si l’observation \(x_{(i)}\) est unique, soit égale au rang moyen de toutes les observations qui lui sont égales. Nous proposons pour la constante de correction \(a\) la valeur \(0,375\) introduite en 1958 par Blom. D’autres valeurs de correction ont été proposées, mais celle de Blom convient très bien, non seulement dans le cas de la normalité, mais aussi en général.

Remarque. Lorsqu’il s’agit de la distribution Normale, ce graphique a été proposé par Henry et s’appelle droite de Henry ; il sera présenté avec les tests de normalité (cf. la page sur les tests d’adéquation).

Exemple. Nous considérons l’Exemple 2 de la durée de vie d’un équipement auquel nous avons appliqué un nouveau procédé permettant de prolonger cette durée de vie. Nous admettons que la durée de vie d’un équipement est distribuée selon une loi exponentielle \({\cal GA}(1\ ;\ \beta)\). Nous notons la prolongation de cette durée de vie, obtenue avec le nouveau procédé, par \(x_0\).

Pour tracer un graphique des quantiles, nous posons \(x_0=2,497\) et \(\beta=1,534\). Ces choix seront analysés dans la page sur les estimateurs sans biais. Nous construisons le graphique avec la commande :

qqplot (Donnees[,2], qgamma ( ppoints (Donnees[,2],3/8), shape =1, rate =1.534)+2.497,
col ="blue", xlab ="Durées observées", ylab ="Gamma(1 ; 1,534)+2,497",
main ="Graphique des quantiles pour les Durées.");
abline (a=0,b=1, col ="red");

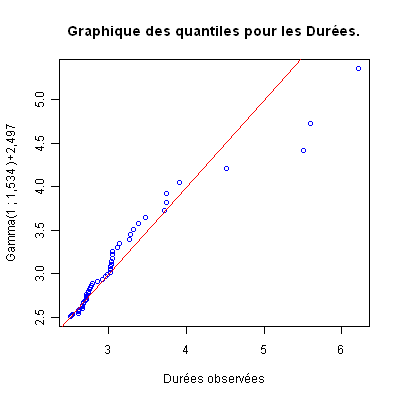
Remarque. C’est la commande ppoints(Donnees[,2],3/8) qui permet de calculer les fréquences cumulées corrigées avec la règle de Blom. La commande abline(a=0,b=1,col="red") permet d’ajouter la première bissectrice.

Interprétation. Nous constatons que les points sont relativement proches de la première bissectrice à l’exception des quatre derniers points qui sont en queue de distribution. La loi \({\cal GA}(1\ ;\ \beta)\) semblerait convenir pour décrire ce phénomène.

Haut de la page.

3. Descriptions graphiques.

3. Descriptions graphiques.

3.6. Graphique des quantiles.