

Les graphiques concernant une variable qualitative ont pour objectif essentiel de présenter de manière claire la distribution des modalités.
Définition 1. Nous appelons graphique à barres le graphique qui, à chaque modalité de la variable, associe un rectangle (barre) dont l’une des dimensions est proportionnelle à la fréquence de la modalité et l’autre identique pour toutes les modalités.
Interprétation. Ce type de graphique permet de mettre en évidence simplement la modalité la plus fréquente, la moins fréquente et d’une manière générale la répartition des modalités.
Application 1. Nous reprenons l’exemple des Sinistres. Nous construisons un graphique à barres pour la variable NATU, nature du sinistre (première colonne du tableau des données), avec la commande suivante :
barplot
(
table
(Donnees[,1]),
width
=1,
space
=0.4,
horiz
=FALSE,
col
="orange",
border
="red",
main
="Fig. 1 : Données Sinistres.",
xlab
="Nature du sinistre",
ylab
="Effectifs");
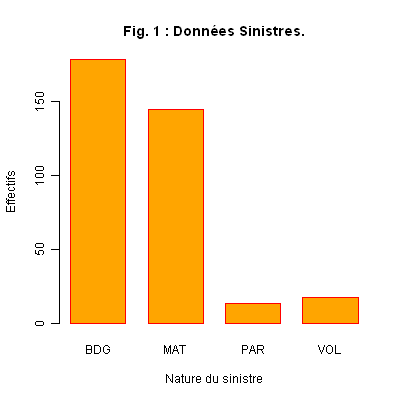
Remarquons la nécessité de créer une table à partir des données brutes avant d’appliquer la commande créant le graphique. Les modalités ont été positionnées dans l’ordre alphabétique. Il est possible de positionner les barres horizontalement, ou encore d’avoir plusieurs barres juxtaposées ou empilées, ainsi que d’autres options.
Interprétation. Nous constatons que la modalité la plus fréquente est la «BDG» (bris de glaces), qui précède tout juste «MAT» (dégats matériels), loin devant les deux dernières modalités «PAR» (parking) et «VOL» (vol).
Lorsque nous avons une variable qualitative ordonnée, il peut être intéressant de construire un graphique avec les fréquences cumulées.
Application 1. Nous reprenons l’exemple des Sinistres. Nous construisons un graphique à barres avec les fréquences cumulées pour la variable RESP, taux de responsabilité du conducteur (sixième colonne du tableau des données), avec la commande suivante :
barplot
(
cumsum
(
table
(Donnees[,6])),
width
=1,
space
=0.4,
horiz
=FALSE,
col
="cyan",
border
="blue",
main
="Fig. 2 : Données Sinistres.",
xlab
="Responsabilité du conducteur",
ylab
="Effectifs cumulés");

Interprétation. Nous constatons que la modalité la plus fréquente est \(0\) % de responsabilité du conducteur ; il y a quelque sinistres avec \(50\) % et un peu plus avec \(100\) % de responsabilité du conducteur ; il n’y a pas eu de sinistres avec \(25\) % et \(75\) % de responsabilité.
Un autre exemple de graphique utile pour des variables qualitatives est le suivant.
Définition 2. Nous appelons graphique à secteurs de cercle le graphique qui est constitué par un cercle et à chaque modalité de la variable est associé un secteur dont l’aire (ou l’angle) est proportionnelle à la fréquence de la modalité.
Application 1. Nous considérons la même variable que la première utilisée ci-dessus. Nous construisons un graphique à secteurs de cercle pour la variable NATU, nature du sinistre, avec la commande suivante :
pie
(
table
(Donnees[,1]),
border
="brown",
main
="Fig. 3 : Données Sinistres.",
sub
="Nature du sinistre");
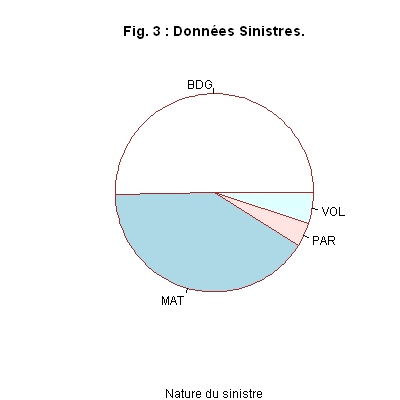
Interprétation. Nous faisons les mêmes commentaires que ci-dessus.
Haut de la page.