3.1. Variable qualitative.
3.2. Variable discrète.
3.3. Variable continue - histogramme.
3.4. Graphique branche et feuilles.
3.5. Graphique boîte à moustaches.
3.6. Graphique des quantiles.
Références bibliographiques.
Notations.
Commandes de R.
Index alphabétique.
Index des Mathématiciens - Statisticiens.
© Photis NOBELIS, 2009 à
.
Ancien Maître de Conférences en Statistique de l'Université Louis Pasteur de Strasbourg.
Je vous remercie de me signaler toutes mes omissions, erreurs, propositions d’amélioration du site, etc. Dans la mesure du possible, si mon temps le permet, je répondrai également à vos questions.
Pour représenter graphiquement une variable discrète nous avons essentiellement un type de diagramme.
Définition 1. Considérons la distribution \(Dist(x_{\bullet})=\lbrace (c_i,\ n_i ), i=1,\ \cdots ,\ r\rbrace\). Nous construisons un graphique de la manière suivante. Nous reportons les modalités \(c_i\) sur l’axe des abscisses et, au-dessus de chacune d’elles, nous traçons un segment vertical d’une hauteur proportionnelle à la fréquence \(f_i\) associée. Ce graphique est appelé le diagramme des fréquences ou en bâtons.
Interprétation. Ce graphique, permet de mettre en évidence la distribution observée des modalités, de situer la zone la plus fréquente, la moins fréquente et d’une manière générale la dispersion des observations.
Exemple. Nous considérons l’Exemple 1 du nombre de personnes absentes par jour dans une entreprise. Nous avons vu qu’il s’agit d’une variable discrète. Nous avions calculé la distribution
| Nombre d’absents | \(0\) | \(1\) | \(2\) | \(3\) | \(4\) | 5 | \(6\) | \(7\) | |||||||||
| Nombre de jours | \(23\) | \(57\) | \(66\) | \(50\) | \(27\) | \(16\) | \(8\) | \(3\) |
Nous construisons un diagramme des fréquences avec la commande suivante :
plot
(
table
(Donnees),
col
="green4",
xlab
="Nombre d'absents par jour",
ylab
="Effectifs",
main
="Fig. 1 : Distribution des fréquences");
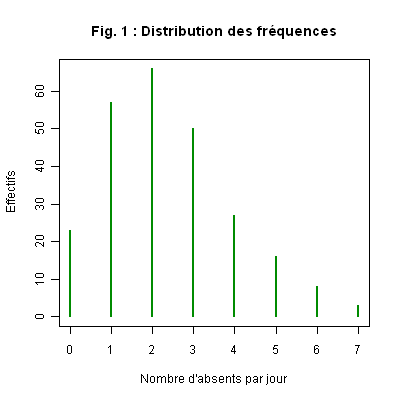
Remarquons la nécessité de créer une table à partir des données brutes avant d’appliquer la commande créant le graphique. Les modalités ont été positionnées dans l’ordre croissant.
Interprétation. Nous constatons que la modalité la plus fréquente est \(2\), il y une forte asymétrie de la distribution ; cette répartition ressemble à une distribution de Poisson.
Nous pouvons également utiliser les fréquences cumulées. Nous avions calculé la distribution de ces effectifs cumulés :
| Nombre d’absents | \(0\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) | \(7\) | |||||||||
| Nombre de jours | \(23\) | \(80\) | \(146\) | \(196\) | \(223\) | \(239\) | \(247\) | \(250\) |
Nous construisons un diagramme des fréquences cumulées. Pour ce faire nous transformons le tableau des contingences cumulées en table de données avec la commande :
Tableau = as.data.frame ( cumsum ( table (Donnees))).
Après transformation des colonnes nous effectuons :
plot
(Tableau[,1],Tableau[,2],
col
="magenta",
type
="h",
xlab
="Nombre d'absents par jour",
ylab
="Effectifs cumulés",
main
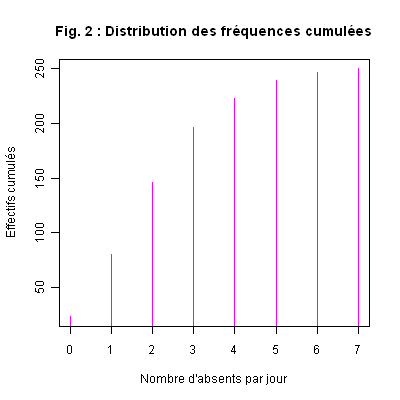
="Fig. 2 : Distribution des fréquences cumulées");
Ce qui nous donne le graphique suivant :
