4.0. Introduction aux lois usuelles.
4.1. Lois indicatrices et associées.
4.2. Lois de Poisson.
4.3. Lois uniformes discrètes.
4.4. Lois Normales et associées.
4.5. Lois Gamma.
4.6. Lois Bêta.
4.7. Lois de Weibull.
4.8. Lois de Pareto.
4.9. Lois de Gumbel.
4.10. Lois de Cauchy.
4.11. Lois uniformes continues.
4.12. Famille exponentielle. \(\ast\)
4.13. Lois empiriques.
4.14. Lois associées à la Statistique d’ordre. \(\ast\)
Références bibliographiques.
Notations.
Commandes de R.
Index alphabétique.
Index des Mathématiciens - Statisticiens.
© Photis NOBELIS, 2009 à
.
Ancien Maître de Conférences en Statistique de l'Université Louis Pasteur de Strasbourg.
Je vous remercie de me signaler toutes mes omissions, erreurs, propositions d’amélioration du site, etc. Dans la mesure du possible, si mon temps le permet, je répondrai également à vos questions.
Nous présentons la famille de lois Bêta liées aux lois Gamma. Pour cela nous introduisons une fonction spéciale.
Définition 1. Nous appelons fonction Bêta incomplète la fonction définie par :
\[ B(t\ ;\ \alpha\ ;\ \beta)=\int_0^tu^{\alpha-1}(1-u)^{\beta-1}du,\quad \forall t\in\rbrack 0\ ;\ 1\lbrack,\quad \alpha,\beta\in{\mathbb R}_+^{\star}. \]Nous notons \(B(\alpha\ ;\ \beta)=B(1\ ;\ \alpha\ ;\ \beta)\) et nous l’appelons fonction Bêta.
Propriété 1. La fonction Bêta est liée à la fonction Gamma de la manière suivante :
\[ B(\alpha\ ;\ \beta)=\frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)}. \]Remarque 1. La fonction Bêta est une généralisation pour des nombres réels non entiers de l’inverse du coefficient binomial. Le logiciel R permet d’obtenir des valeurs de Bêta :
beta(0.5,1.5) ; réponse : 1.570796.
Définition 2. Une v.a. \(X\) suit une loi Bêta, de paramètres \(\alpha,\ \beta \in {\mathbb R}_+^{\star}\), si elle admet pour densité de probabilité la fonction :
\[ f_X(t) =\cases{ \displaystyle\frac{1}{B(\alpha\ ;\ \beta)}t^{\alpha-1}(1-t)^{\beta-1} & \( {\it si}\quad t\in\rbrack 0\ ;\ 1\lbrack\),\cr 0 & \( {\it si}\quad t\notin\rbrack 0\ ;\ 1\lbrack \). } \]Ceci est noté \({\cal L}(X)={\cal BE}(\alpha\ ;\ \beta)\). La loi \({\cal BE}(1\ ;\ 1)={\cal U}(\rbrack 0\ ;\ 1\lbrack)\) est la loi Uniforme sur l’intervalle \(\rbrack 0\ ;\ 1\lbrack\).
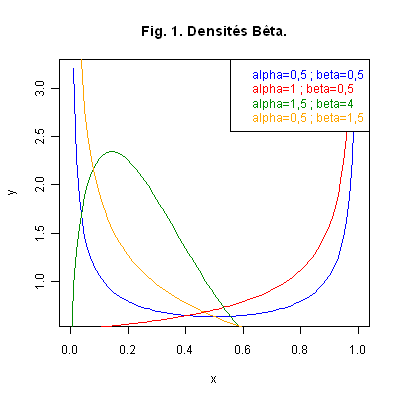
Modélisation. La loi Bêta, outre ses aspects théoriques, présente un intérêt certain. Comme le montre le graphique ci-dessous, elle admet différentes asymétries sur l’intervalle \(\rbrack 0\ ;\ 1\lbrack\), selon les valeurs des paramètres. Elle apparaît également lors de l’observation de lois de Bernoulli pour modéliser la variation de leurs paramètres lorsque ces derniers sont aléatoires. Enfin les lois Bêta apparaissent dans l’étude des statistiques d’ordre.
Graphique 1. La Fig. 1 ci-dessous représente les courbes des densités de loi Beta \({\cal BE}(0,5 \ ;\ 0,5)\), \({\cal BE}(1\ ;\ 0,5)\), \({\cal BE}(1,5\ ;\ 4)\) et \({\cal BE}(0,5\ ;\ 1,5)\). Nous voyons évoluer l’allure de la densité en fonction des paramètres.
Calculs avec R. A la base, les commandes comprennent l’expression beta précédée d’une lettre spécifiant le calcul à réaliser. Les options shape1 et shape2 de la commande correspondent respectivement à \(\alpha\) et \(\beta\). Par exemple, si \({\cal L}(X)={\cal BE}(0,5\ ;\ 1,5)\), alors \(f_X(0,8)\) se détermine avec la commande
dbeta(.8,shape1=.5,shape2=1.5) ; réponse : 0.3183099.
Pour calculer \(P(X\leq 0,8)\) nous utilisons la commande
pbeta(.8,shape1=.5,shape2=1.5,lower.tail=TRUE) ; réponse : 0.9594807.
Pour calculer la médiane nous utilisons la commande
qbeta(0.5,shape1=.5,shape2=1.5,lower.tail=TRUE) ; réponse : 0.163194.
Il est possible de réaliser des simulations d’observations d’une loi Bêta avec la commande rbeta et les paramètres souhaités.
Propriété 2. Si \({\cal L}(X)={\cal BE}(\alpha\ ;\ \beta)\) alors :
\[ {\mathbb E}\lbrack X \rbrack = \frac{\alpha}{\alpha+\beta},\quad \sigma^2\lbrack X\rbrack =\frac{\alpha\beta}{(\alpha+\beta)^2(1+\alpha+\beta)},\quad \mu^{\prime}_k\lbrack X\rbrack={\mathbb E}\lbrack X^k \rbrack=\frac{B(\alpha+k\ ;\ \beta)}{B(\alpha\ ;\ \beta)} \]et pour \( \alpha, \beta \in\rbrack 0\ ;\ +\infty\lbrack\),
\[ Mo\lbrack X\rbrack=\cases{ 0 & \({\it si}\quad \alpha\in \rbrack 0\ ;\ 1\lbrack,\ \beta\in\lbrack 1\ ;\ +\infty\lbrack\),\cr 1 & \({\it si}\quad \alpha\in \lbrack 1\ ;\ +\infty\lbrack,\ \beta\in\rbrack 0\ ;\ 1\lbrack,\)\cr 0\ {\it et}\ 1 & \( {\it si}\quad \alpha,\ \beta \in \rbrack 0\ ;\ 1\lbrack,\)\cr \dfrac{\alpha-1}{\alpha+\beta-2} & \({\it si}\quad \alpha,\ \beta \in \rbrack 1\ ;\ +\infty\lbrack\). } \]Propriété 3. Si \({\cal L}(X)={\cal BE}(\alpha\ ;\ \beta)\) alors la f.r. \( F_X(t)= P(X\leq t)\) est la fonction bêta incomplète normalisée sur l’intervalle \(\rbrack 0, 1\lbrack\) ; de plus :
\[ F_X(t) =\cases{ 0 & \(t\leq 0,\) \cr \displaystyle\frac{B(t\ ;\ \alpha\ ;\ \beta)}{B(\alpha\ ;\ \beta)} & \( {\it si}\quad t\in\rbrack 0\ ;\ 1\lbrack,\)\cr 1 & \( {\rm si}\quad 1\leq t \). } \]Il est possible, lorsque \(\alpha,\ \beta\) sont des nombres entiers, d’écrire la f.r. sous forme de somme (cf. propriété 2 des statistiques d’ordre).
Propriété 4. Si \({\cal L}(X)={\cal BE}(\alpha\ ;\ \beta)\) alors \({\cal L}(1-X)={\cal BE}(\beta\ ;\ \alpha)\).
Propriété 5. Soit deux v.a. \(X,\ Y\) indépendantes et telles que \({\cal L}(X)={\cal GA}(\alpha_1\ ;\ \beta)\) et \({\cal L}(Y)={\cal GA}(\alpha_2\ ;\ \beta)\), alors
\[ {\cal L}\left(\frac{X}{X+Y}\right)={\cal BE}(\alpha_1\ ;\ \alpha_2). \]Remarque 2. En utilisant la propriété précédente dans le cadre de lois du khi-deux, il est possible de considérer des lois Bêta excentrées. Les calculs dans R se font alors en ajoutant dans la commande l’option ncp qui permet de donner le paramètre d’excentricité. Ce type de propriété nous permet de définir une loi Bêta de dimension deux.
Propriété 6. Soit trois v.a. \(X,\ Y,\ Z\) indépendantes et telles que \({\cal L}(X)={\cal GA}(\alpha_1\ ;\ \beta)\), \({\cal L}(Y)={\cal GA}(\alpha_2\ ;\ \beta)\) et \({\cal L}(Z)={\cal GA}(\alpha_3\ ;\ \beta)\). Nous posons :
\[ U=\frac{X}{X+Y+Z}\quad {\it et}\quad V=\frac{X+Y}{X+Y+Z}. \]Le couple \((U,\ V)\) admet pour densité la fonction :
\[ f_{(U,\ V)}(u,\ v) =\frac{\Gamma(\alpha_1+\alpha_2+\alpha_3)}{\Gamma(\alpha_1)\Gamma(\alpha_2)\Gamma(\alpha_3)}u^{\alpha_1-1}(v-u)^{\alpha_2-1}(1-v)^{\alpha_3-1} I_{\lbrace 0\leq u\leq v\leq 1\rbrace}(u,\ v). \]Définition 3. Nous appelons fonction Bêta de dimension deux la fonction définie par :
\[ B_2(\alpha_1\ ;\ \alpha_2\ ;\ \alpha_3)=\frac{\Gamma(\alpha_1)\Gamma(\alpha_2)\Gamma(\alpha_3)}{\Gamma(\alpha_1+\alpha_2+\alpha_3)},\quad \alpha_1,\ \alpha_2,\ \alpha_3\in{\mathbb R}_+^{\star}. \]Nous disons que le couple \((U, V)\) suit une loi Bêta de dimension deux et nous notons \({\cal L}((U, V))={\cal BE}_2(\alpha_1\ ;\ \alpha_2\ ;\ \alpha_3)\).
La f.r. du couple, sur le triangle \({\lbrace 0\leq u\leq v\leq 1\rbrace}\), est la fonction Bêta incomplète régularisée de dimension deux. Lorsque les paramètres sont des nombres entiers elle peut s’exprimer comme une somme (cf. propriété 5 des statistiques d’ordre). Les caractéristiques essentielles de cette loi sont :
Propriété 7. Si \({\cal L}((U, V))={\cal BE}_2(\alpha_1\ ;\ \alpha_2\ ;\ \alpha_3)\) alors :
\[ {\mathbb E}\lbrack U \rbrack = \frac{\alpha_1}{\alpha_1+\alpha_2+\alpha_3},\quad \sigma^2\lbrack U\rbrack =\frac{\alpha_1(\alpha_2+\alpha_3)}{(\alpha_1+\alpha_2+\alpha_3)^2(1+\alpha_1+\alpha_2+\alpha_3)}, \quad {\mathbb E}\lbrack V \rbrack = \frac{\alpha_1+\alpha_2}{\alpha_1+\alpha_2+\alpha_3},\quad \sigma^2\lbrack V\rbrack =\frac{(\alpha_1+\alpha_2)\alpha_3}{(\alpha_1+\alpha_2+\alpha_3)^2(1+\alpha_1+\alpha_2+\alpha_3)}, \] \[ {\mathbb C}ov\lbrack U,\ V\rbrack=\frac{\alpha_1\alpha_3}{(\alpha_1+\alpha_2+\alpha_3)^2(1+\alpha_1+\alpha_2+\alpha_3)}\quad {\it et} \quad \varrho\lbrack U,\ V\rbrack=\sqrt{\frac{\alpha_1\alpha_3}{(\alpha_1+\alpha_2)(\alpha_2+\alpha_3)}}. \] Haut de la page.