Contre-hypothèses intervalles.

7.4.3. Contre-hypothèses de type intervalles finis.

Soit \(X\) une v.a. dont la loi \({\cal L}(X)\) appartient à la famille exponentielle à un paramètre unidimensionnel \(\theta\in\Theta \subset{\mathbb R}\) ; c’est-à-dire que, soit dans le cas discret soit dans le cas continu, la loi \({\cal L}_{\theta}\) est donnée par :

\[ \ln(l_{\theta}(x))=a(\theta)b(x)+c(\theta)+d(x). \]

Lorsque nous observons une réalisation \(x_{\bullet}=(x_1, \cdots, x_n)\) d’un \(n\)-échantillon de \(X\), la vraisemblance s’écrit :

\[ \ln(L(x_{\bullet}\ ;\ \theta))=a(\theta)T(x_{\bullet})+nc(\theta)+\sum_{j=1}^nd(x_j), \]

avec \(T(x_{\bullet})=\displaystyle\sum_{j=1}^nb(x_j)\). Nous supposons \(a(\theta)\) strictement monotone.

Propriété 1. Soit \({\mathfrak L}\) une famille exponentielle à rapport de vraisemblance monotone par rapport à la statistique \(T(X_{\bullet})\). Soit \(\theta_1, \theta_2\in\Theta\) avec \(\theta_1 < \theta_2\) et un seuil \(\alpha\in\rbrack 0\ ;\ 1\lbrack\) fixés. Le test \(\psi^{\star}\) défini par :

\[ \psi^{\star}(x_{\bullet})=\gamma_1I_{\lbrace T(x_{\bullet})=c_1\rbrace}(x_{\bullet})+I_{\lbrace c_1 < T(x_{\bullet}) < c_2\rbrace}(x_{\bullet})+\gamma_2I_{\lbrace T(x_{\bullet})=c_2\rbrace}(x_{\bullet}), \]

où les constantes \(\gamma_1, \gamma_2, c_1\) et \(c_2\) sont déterminées par les contraintes \({\mathbb E}_{\theta_1}\lbrack \psi^{\star}(X_{\bullet})\rbrack={\mathbb E}_{\theta_2}\lbrack \psi^{\star}(X_{\bullet})\rbrack=\alpha\), satisfait aux relations suivantes :

\({\mathbb E}_{\theta}\lbrack\psi^{\star}(X_{\bullet})\rbrack \geq {\mathbb E}_{\theta}\lbrack\psi(X_{\bullet})\rbrack\), pour tout \(\theta \in \rbrack \theta_1\ ;\ \theta_2\lbrack\) et tout \(\psi\) tel que \({\mathbb E}_{\theta_1}\lbrack\psi(X_{\bullet})\rbrack={\mathbb E}_{\theta_2}\lbrack\psi(X_{\bullet})\rbrack=\alpha\).
\({\mathbb E}_{\theta}\lbrack\psi^{\star}(X_{\bullet})\rbrack \leq {\mathbb E}_{\theta}\lbrack\psi(X_{\bullet})\rbrack\), pour tout \(\theta \not\in \rbrack \theta_1\ ;\ \theta_2\lbrack\) et tout \(\psi\) tel que \({\mathbb E}_{\theta_1}\lbrack\psi(X_{\bullet})\rbrack={\mathbb E}_{\theta_2}\lbrack\psi(X_{\bullet})\rbrack=\alpha\).
\({\mathbb E}_{\theta}\lbrack\psi^{\star}(X_{\bullet})\rbrack\leq \alpha\) pour tout \(\theta \not\in \rbrack \theta_1\ ;\ \theta_2\lbrack\).
\({\mathbb E}_{\theta}\lbrack\psi^{\star}(X_{\bullet})\rbrack\geq \alpha\) pour tout \(\theta \in \rbrack \theta_1\ ;\ \theta_2\lbrack\).

Fixons \(\theta\) tel que \(\theta \in \rbrack \theta_1\ ;\ \theta_2\lbrack\). Pour déterminer le maximum de \({\mathbb E}_{\theta}\lbrack\psi(X_{\bullet})\rbrack\) sous les contraintes \({\mathbb E}_{\theta_1}\lbrack \psi(X_{\bullet})\rbrack={\mathbb E}_{\theta_2}\lbrack \psi(X_{\bullet})\rbrack=\alpha\), il suffit de déterminer, pour deux constantes \(k_1, k_2\), le maximum de \({\mathbb E}_{\theta}\lbrack\psi(X_{\bullet})\rbrack-k_1{\mathbb E}_{\theta_1}\lbrack\psi(X_{\bullet})\rbrack-k_2{\mathbb E}_{\theta_2}\lbrack\psi(X_{\bullet})\rbrack\) sous les mêmes contraintes. Ce maximun est atteint pour :

\[ \psi^{\star}(x_{\bullet})=\sum_{i=1}^2\gamma_iI_{\lbrace L(x_{\bullet, i} ; \theta)=k_1L(x_{\bullet, i} ; \theta_1)+k_2L(x_{\bullet, i}; \theta_2)\rbrace}(x_{\bullet}) + I_{\lbrace L(x_{\bullet} ; \theta)> k_1L(x_{\bullet} ; \theta_1)\rbrace+k_2L(x_{\bullet} ; \theta_2)\rbrace}(x_{\bullet}). \]

Nous sommons sur l’ensemble des points \(x_{\bullet ,j}\) où \(L(x_{\bullet, j} ; \theta)=k_1L(x_{\bullet, j} ; \theta_1)+k_2L(x_{\bullet, j}; \theta_2)\) ; nous constatons par la suite qu’il n’y en a que deux. Les constantes \(\gamma_1, \gamma_2, k_1\) et \(k_2\) sont déterminées par les relations \({\mathbb E}_{\theta_1}\lbrack \psi^{\star}(X_{\bullet})\rbrack= {\mathbb E}_{\theta_2}\lbrack \psi^{\star}(X_{\bullet})\rbrack=\alpha\). Le fait que le rapport de vraisemblance soit monotone par rapport à la statistique \(T(x_{\bullet})=\sum_{j=1}^nb(x_j)\) et l’étude de la fonction exponentielle impliquent la forme de \(\psi^{\star}(x_{\bullet})\) qui ne dépend plus que de \(\theta_1\) et de \(\theta_2\) et qui est celle de l’énoncé, avec les mêmes contraintes. C’est le test recherché. La deuxième inégalité s’obtient de manière analogue. Les deux autres résultats découlent d’un calcul direct des espérances en utilisant la forme de \(\psi^{\star}(x_{\bullet})\) avec les vraisemblances.\(\quad \square\)

Alternative 4.

Soit \({\mathfrak L}\) une famille exponentielle paramètrique dont le paramètre \(\theta\in\Theta \subset{\mathbb R}\) ; nous fixons \(\theta_1, \theta_2\in\Theta\), avec \(\theta_1 < \theta_2\). Nous considérons l’alternative :

\({\cal H}_0^{(4)}=\lbrace \theta \not\in \rbrack \theta_1\ ;\ \theta_2\lbrack\rbrace\quad\) contre \(\quad{\cal H}_1^{(4)}=\lbrace \theta\in\rbrack \theta_1\ ;\ \theta_2\lbrack\rbrace\).

Pour \(\theta^{\prime},\ \theta^{\prime\prime}\in\Theta\), avec \(\theta_1 < \theta^{\prime} < \theta^{\prime\prime} <\theta_2 \), nous considérons également les alternatives dont l’hypothèse nulle est soit \({\cal H}_0^{(4)}=\lbrace \theta \not\in \rbrack \theta_1\ ;\ \theta_2\lbrack\rbrace\), soit l’une des hypothèses, encore notées \({\cal H}_0^{(4)}\),

\({\cal H}_0^{(4)}=\lbrace \theta=\theta_1\rbrace\cup\lbrace\theta_2\leq \theta\rbrace,\quad {\cal H}_0^{(4)}=\lbrace \theta\leq \theta_1\rbrace\cup\lbrace\theta=\theta_2\rbrace,\quad {\cal H}_0^{(4)}=\lbrace \theta=\theta_1, \theta_2\rbrace\),

et la contre-hypothèse est soit \({\cal H}_1^{(4)}=\lbrace \theta\in\rbrack \theta_1\ ;\ \theta_2\lbrack\rbrace\), soit l’une des hypothèses encore notées \({\cal H}_1^{(4)}\),

\({\cal H}_1^{(4)}=\lbrace \theta\in\rbrack \theta^{\prime}\ ;\ \theta_2\lbrack\rbrace,\quad {\cal H}_1^{(4)}=\lbrace \theta\in\rbrack \theta_1\ ;\ \theta^{\prime\prime}\lbrack\rbrace,\quad {\cal H}_1^{(4)}=\lbrace \theta\in\rbrack \theta^{\prime}\ ;\ \theta^{\prime\prime}\lbrack\rbrace\).

Sauf confusions possibles, chacune de ces seize alternatives sera toujours appelée Alternative 4. C’est la première alternative qui représentera cet ensemble d’alternatives.

Remarque 1. Si pour l’utilisateur décider à tort que le paramètre est dans un intervalle fixé a les conséquences les plus défavorables, c’est sur ce test \(\psi^{(4)}(X_{\bullet})\) qu’il doit fonder sa démarche.

Propriété 2. Soit \({\mathfrak L}\) une famille exponentielle à un paramètre unidimensionnel \(\theta\in\Theta \subset{\mathbb R}\) à rapport de vraisemblance monotone par rapport à la statistique \(T(X_{\bullet})\). Soit \(\alpha\in \rbrack 0\ ;\ 1\lbrack\) un seuil fixé. Pour tester chacune des seize Alternatives 4 ci-dessus, nous considérons le même test :

\[ \psi^{(4)}(x_{\bullet})=\gamma_1I_{\lbrace T(x_{\bullet})=c_1\rbrace}(x_{\bullet})+I_{\lbrace c_1 < T(x_{\bullet}) < c_2\rbrace}(x_{\bullet})+\gamma_2I_{\lbrace T(x_{\bullet})=c_2\rbrace}(x_{\bullet}), \]

où les constantes \(\gamma_1, \gamma_2, c_1\) et \(c_2\) sont déterminées par les relations :

\[ {\mathbb E}_{\theta_i}\lbrack \psi^{(4)}(X_{\bullet})\rbrack= \gamma_1P_{\theta_i}\Big(T(X_{\bullet})=c_1\Big) + P_{\theta_i}\Big(c_1 < T(X_{\bullet}) < c_2\Big)+\gamma_2P_{\theta_i}\Big(T(X_{\bullet})=c_2\Big)=\alpha,\ i=1,\ 2. \]

Pour chacune des alternatives, ce test est de seuil \(\alpha\), sans biais, U.P.P. à ce seuil et convergent. La fonction puissance \({\mathbb E}_{\theta}\lbrack\psi^{(4)}(X_{\bullet})\rbrack\) n’est définie que pour \(\theta\in{\cal H}_0^{(4)}\bigcup{\cal H}_1^{(4)}\) dans chaque alternative. Ainsi la procédure optimale de décision se résume de la maniètre suivante :

Si \(T(x_{\bullet}) < c_1\) ou si \(T(x_{\bullet}) > c_2\), nous décidons «\({\cal H}_0^{(4)}\) est vraie».
Si \(T(x_{\bullet}) = c_i\), nous décidons «\({\cal H}_1^{(4)}\) est vraie» avec une probabilité \(\gamma_i\) ;
nous réalisons \(u\) de loi \({\cal U}(\rbrack 0\ ;\ 1\lbrack)\) et si \(u < \gamma_i\) nous décidons «\({\cal H}_1^{(4)}\) est vraie», si \(u \geq \gamma_i\) nous décidons «\({\cal H}_0^{(4)}\) est vraie» ; ceci pour \(i=1,\ 2\).
Si \(c_1 < T(x_{\bullet}) < c_2\), nous décidons «\({\cal H}_1^{(4)}\) est vraie».

Cet énoncé est une conséquence directe de la Propriété 1 ci-dessus, ainsi que de la Propriété 2 et de la Propriété 3 du test fondamental. \(\quad \square\)

Remarque 2. Si nous étudions une loi continue alors \(P_{\theta_i}(T(X_{\bullet})=c_{i^{\prime}})=0\), pour \(i,\ i^{\prime}=1,\ 2\). En pratique, nous pouvons, pour ne pas avoir \(T(x_{\bullet})=c_i,\ i=1,\ 2\), calculer \(T(x_{\bullet})\) avec un chiffre décimal de plus que \(c_i,\ i=1,\ 2\) ou inversement. Nous pouvons également fixer \(\gamma_i=0,\ i=1,\ 2\), cela ne change rien aux propriétés du test. Nous décidons alors :

«\({\cal H}_0^{(4)}\) est vraie» si \(T(x_{\bullet}) \leq c_1\) ou si \(T(x_{\bullet}) \geq c_2\),
«\({\cal H}_1^{(4)}\) est vraie» si \(c_1 < T(x_{\bullet}) < c_2\).

Dans le cas discret, en général \(P_{\theta_i}(T(X_{\bullet})=c_{i^{}\prime}) > 0\), pour \(i,\ i^{\prime}=1,\ 2\). Cependant nous pouvons, pour faciliter les calculs, poser \(\gamma_i=0\), \(i=1,\ 2\). La décision se prendra de la même manière que ci-dessus, mais le seuil sera inférieur à \(\alpha\) et nous perdrons légèrement de la puissance.

Exemple. Un lot de billes d’acier est livré dans une usine de fabrication de roulements. Un contrôle de réception sur le diamètre des billes, noté \(\mu\) et mesuré en mm, est mis en place. Nous désignons par \(\mu_1\) (resp. \(\mu_2\)) la valeur minimale (resp. maximale) du diamètre d’une bille en dessous (resp. au dessus) de laquelle le roulement ne fonctionne pas correctement. Comme l’arrêt de la chaîne de production a des conséquences plus graves pour l'usine que le refus à tort d’une livraison, suivant notre principe de choix de l’alternative, nous testons :

\({\cal H}_0^{(4)}=\lbrace \mu \not\in \rbrack \mu_1\ ;\ \mu_2\lbrack\rbrace\quad\) contre \(\quad{\cal H}_1^{(4)}=\lbrace \mu\in\rbrack \mu_1\ ;\ \mu_2\lbrack\rbrace\).

Nous supposons que le diamètre d’une bille d’acier choisie au hasard dans l’ensemble des billes est une réalisation d’une v.a. \(X\) qui suit la loi Normale \({\cal L}(X)={\cal N}(\mu\ ;\ \sigma^2)\), où \(\sigma^2\) est une caractéristique connue de la production. Il s’agit d’une loi continue et sa densité vérifie :

\[ f(t\ ;\ \mu)=\exp(\frac{t\mu}{\sigma^2}-\frac{\mu^2}{2\sigma^2}-\ln(\sigma\sqrt{2\pi}) -\frac{t^2}{2\sigma^2}). \]

Nous constatons que nous sommes en présence d’une famille exponentielle à un paramètre inconnu \(\mu\) avec un rapport de vraisemblance croissant vis-à-vis de la statistique \(T(X_{\bullet})=\overline{X}\). Nous mettons en œuvre le test \(\psi^{(4)}\). Ainsi nous décidons :

«\({\cal H}_0^{(4)}\) est vraie» si \(\overline{x} \not\in \rbrack c_1\ ;\ c_2\lbrack\),
«\({\cal H}_1^{(4)}\) est vraie» si \(\overline{x} \in \rbrack c_1\ ;\ c_2\lbrack\),

où les constantes sont déterminées par les deux contraintes \(P_{\mu_i}(c_1 \leq \overline{X} \leq c_2)=\alpha,\ i=1, 2\), pour un seuil donné \(\alpha\). Le graphique des densités des lois \({\cal N}(\mu_1\ ;\ \sigma^2)\) et \({\cal N}(\mu_2\ ;\ \sigma^2)\) nous montre que les points \(c_1\) et \(c_2\) sont symétriques de part et d’autre de \(\dfrac{\mu_1+\mu_2}{2}\), c’est-à-dire qu’il existe un nombre \(z\) tel que :

\[ c_1=\frac{\mu_1+\mu_2}{2}-z,\quad c_2=\frac{\mu_1+\mu_2}{2}+z. \]

Donc, en écrivant la contrainte pour \(\mu_1\) (avec \(\mu_2\) le résultat est identique) et après centrage et réduction, nous devons déterminer un nombre \(z_{\alpha}\) tel que :

\[ g(z_{\alpha})=P_{\mu_1}(\frac{\mu_1+\mu_2}{2}-z_{\alpha}\leq \overline{X}\leq\frac{\mu_1+\mu_2}{2}+z_{\alpha})= P(\frac{\sqrt{n}(\mu_2-\mu_1)}{2\sigma}-z_{\alpha}\frac{\sqrt{n}}{\sigma}\leq Z\leq\frac{\sqrt{n}(\mu_2-\mu_1)}{2\sigma}+z_{\alpha}\frac{\sqrt{n}}{\sigma})=\alpha, \]

où la v.a. \(Z\) suit la loi Normale Standard. Comme la fonction \(g(z)\) satisfait à \(g(0)=0\) et \(\displaystyle\lim_{z\rightarrow +\infty}g(z)=1\), nous sommes assurés de l’existence de \(z_{\alpha}\).

Les données de fabrication sont \(\mu_1=10\) ; \(\mu_2=10,2\) et \(\sigma=0,2\). Nous avons observé \(n=50\) billes et \(\overline{x}=10,125\). Nous fixons \(\alpha=0,05\). Nous calculons :

\[ \dfrac{\sqrt{n}(\mu_2-\mu_1)}{2\sigma}=3,535534\quad {\rm et}\quad \dfrac{\sqrt{n}}{\sigma}=35,35534. \]

Le nombre \(z_{0,05}\) doit vérifier \(P(3,535534-z_{0,05}35,35534\leq Z\leq 3,535534+z_{0,05}35,35534)=0,05\). Mais la commande qnorm de R nous donne \(P(4\leq Z)=0\) et \(P(1,645\leq Z)=0,05\). Nous en déduisons \(3,535534-z_{0,05}35,35534=1,645\), c’est-à-dire \(z_{0,05}=0,05347237\) ; finalement :

\[ c_1=10,1-0,05347237\approx 10,04652\quad c_2=10,1+0,05347237\approx 10,15347. \]

La moyenne observée est \(\overline{x}=10,125\). Ainsi nous décidons «\({\cal H}_1^{(4)}=\lbrace \mu\in\rbrack \mu_1\ ;\ \mu_2\lbrack\rbrace\) est vraie», ainsi nous acceptons le lot. Le risque associé à cette décision est inférieur à \(\alpha= 0,05\). Nous pouvons faire confiance à notre décision.

Ce test est de seuil \(0,05\), sans biais, U.P.P. et convergent. Le graphique ci-dessous donne la partie essentielle de la fonction puissance du test \(pu_{\psi^{(4)}}(\mu)={\mathbb E}_{\mu}\lbrack\psi^{(4)}(X_{\bullet})\rbrack=P_{\mu}(c_1\leq \overline{X}\leq c_2)\).

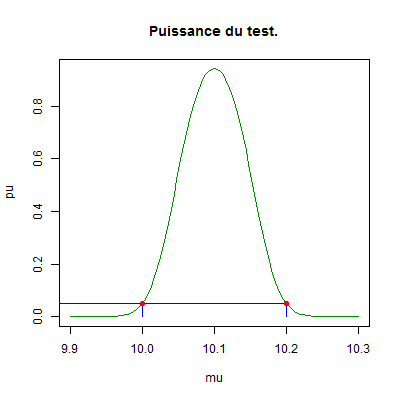
Nous avons marqué en rouge les points de coordonnées \((\mu_1\ ;\ \alpha)=(10\ ;\ 0,05)\) et \((\mu_2\ ;\ \alpha)=(10,2\ ;\ 0,05)\). Les propriétés du test sont bien illustrées. \(\quad \square\)

Références. Une étude complète des tests paramétriques se trouve dans les ouvrages de C. Fourgeaud, A. Fuchs (1967) et de E. L. Lehmann, J. P. Romano (2005).

Haut de la page.

7. Tests classiques d’hypothèses.

7. Tests classiques d’hypothèses.

7.4.3. Contre-hypothèses de type intervalles finis.